Hình bình hành ABCD.Vẽ đg thẳng d ko cắt cạnh nào của hình bình hành.Vẽ AH,BK,CI,DE vuông góc vs d.C/m AH+CI=BK+DE
Ai giỏi toán thì giúp mik vs.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 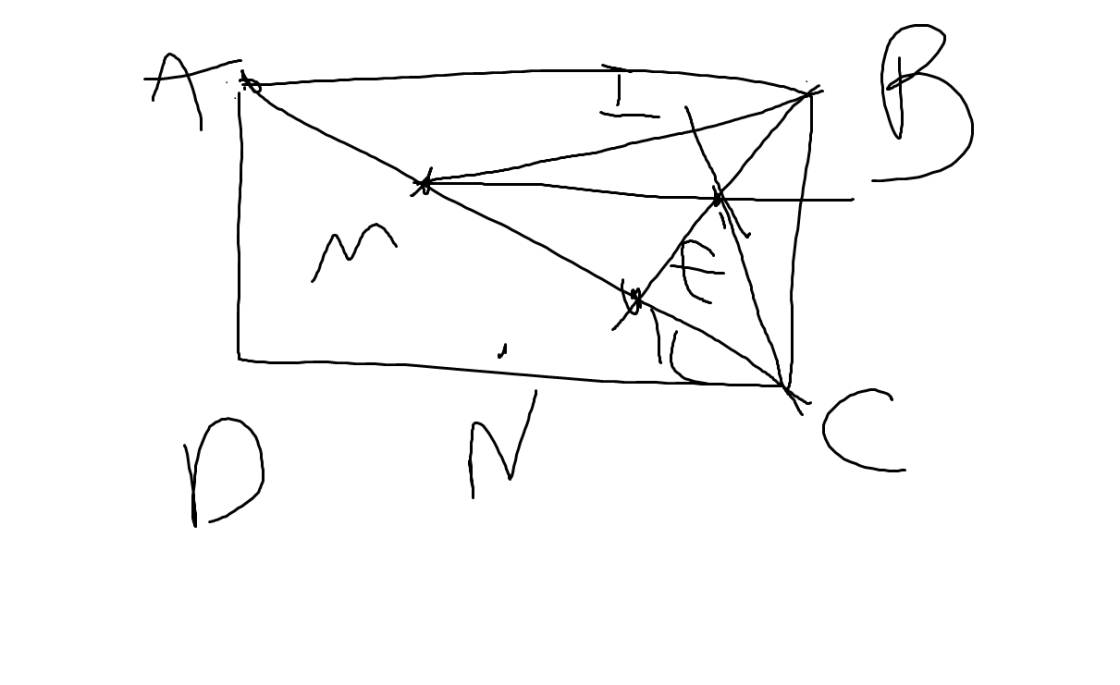
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB

a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông cân tại C

a, Xét tg AHD và tg CIB có \(AD=BC;\widehat{AHD}=\widehat{CIB}=90^0;\widehat{ADH}=\widehat{CBI}\left(so.le.trong\right)\) nên \(\Delta AHD=\Delta CIB\left(ch-gn\right)\)
Do đó \(AH=CI\)
Mà AH//CI (⊥BD) nên AHCI là hbh
b, Vì AHCI là hbh mà M là trung điểm HI nên cũng là trung điểm AC
Do đó A đối xứng C qua M

a)
Ta có: ΔABC cân tại A(gt)
mà AM là đường phân giác ứng với cạnh đáy BC(gt)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
\(\Leftrightarrow AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(cmt)
BK là đường cao ứng với cạnh AC(Gt)
AM cắt BK tại I(Gt)
Do đó: I là trực tâm của ΔBAC(Tính chất ba đường cao của tam giác)
Suy ra: CI\(\perp\)AB(Đpcm)

a) Tam giác ABC cân tại A có AM là phân giác, do đó AM cũng là đường cao
AM vuông góc với BC
Lại có BK vuông góc với AC
Do đó I là trực tâm của tam giác ABC
Vậy CI vuông góc với AB
b) Tam giác BDH = tam giác DBP (ch.gn)
Do đó BH = DP
BDKQ là hình chữ nhật => DP = HK
=> BK = BH + HK = DP + DQ (đpcm)

a: Xét ΔABC có
AM,BK là đường cao
AM cắt BK tại I
=>I là trực tâm
=>CI vuông góc AB tại N
b:
Xet ΔAKB vuông tại K và ΔANC vuông tại N có
AB=AC
góc KAB chung
=>ΔAKB=ΔANC
=>BK=CN
DP//NC
=>DP/NC=BD/BC
=>DP/BK=BD/BC
DQ//BK
=>DQ/BK=CD/CB
=>DQ+DP=BK(BD/BC+CD/CB)=BK

Áp dụng định lí Py-ta-go cho hai tam giác vuông AKH và AIH, ta có:
\(AK^2+HK^2=AH^2\)
\(AI^2+HI^2=AH^2\)
\(\Rightarrow AK^2+HK^2=AI^2+HI^2\) \(\left(\cdot\right)\)
Giả sử \(AB\ne AC\)ta xét 2 trường hợp:
T/hợp 1: \(AB>AC\)
\(\Rightarrow AB-BK>AC-CI\)( vì \(BK=CI\)) hay \(AK>AI\) \(\left(1\right)\)
Mặt khác, vì \(AB>AC\)nên \(HB>HC\)( quan hệ đường xiên - hình chiếu )
\(\Rightarrow HB^2>HC^2\)hay \(HK^2+BK^2>HI^2+CI^2\Rightarrow HK>HI\) \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)suy ra: \(AK^2+HK^2>AI^2+HI^2\): trái với \(\left(\cdot\right)\)
T/hợp 2: \(AB< AC\): Chứng minh tương tự ta có: \(AK^2+HK^2< AI^2+HI^2\): trái với \(\left(\cdot\right)\)
Vậy điều giả sử \(AB\ne AC\)là sai, hay \(AB=AC\)