Cho 3 số trên bảng: 17; 6; 23. Mỗi lần thực hiện ta xoá đi một số và thay bằng tổng hai số còn lại. Hỏi sau một số bước thực hiện như vậy ta có thể nhận được ba số trên bảng là:1945; 1975 và 2023 được hay không? Giải thích vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
4
CM
20 tháng 1 2019
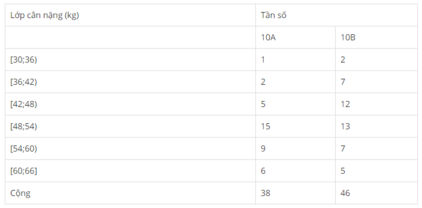
Cân nặng của các học sinh lớp 10A và 10B trường Trung học phổ thông L.
| Lớp cân nặng (kg) | Tần số | |
| 10A | 10B | |
| [30;36) | 2,63 | 4,35 |
| [36;42) | 5,26 | 15,22 |
| [42;48) | 13,16 | 26,08 |
| [48;54) | 39,48 | 28,26 |
| [54;60) | 23,68 | 15,22 |
| [60;66] | 15,79 | 10,87 |
| Cộng | 100 (%) | 100 (%) |
HQ
Hà Quang Minh
Giáo viên
27 tháng 11 2023
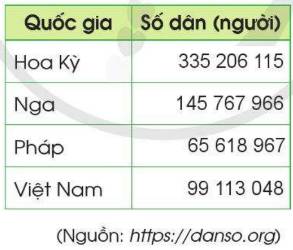
- Những quốc gia có số dân nhiều hơn 100 triệu: Hoa Kỳ, Nga
- Những quốc gia có số dân ít hơn 100 triệu: Pháp, Việt Nam
- Đọc tên các quốc gia theo thứ tự từ quốc gia có đông dân nhất đến quốc gia có ít dân nhất: Hoa Kỳ, Nga, Việt Nam, Pháp.
VM
8 tháng 5 2020
Nhận xét. Sau mỗi lần thực hiện trò chơi thì trên bảng giảm đi một số (xóa 2 số cũ và viết thêm 1 số mới). Sau 9 lần thì trên bảng còn đúng 1 số. Thử chơi: xóa cặp số 9, 10 và thay bằng hiệu 1. Tương tự như các cặp số 1, 2 hoặc 3, 4 hoặc 5, 6 hoặc 7, 8 thì sau 5 lần thực hiện trò chơi, trên bảng còn lại 5 số 1. Thử tiếp 2 lần cặp 1, 1 ta còn 3 số trên bảng là 0, 0, 1. Sau 2 lần chơi nữa ta được số còn lại là 1, khác 0. Vậy bất biến ở đây là gì?
Giải. Tổng 10 số ban đầu là S = 1 + 2 +... + 10 = 55.
Mỗi lần chơi xóa đi hai số a và b bất kỳ rồi viết lên bảng số a - b, ta thấy a + b = (a - b) + 2b. Nghĩa là số mới viết bé hơn tổng hai số vừa xóa là 2b, là một số chẵn. Tức là sau mỗi lần chơi, tổng các số trên bảng luôn là số lẻ. Vậy số cuối cùng cũng là số lẻ.
Chúc bạn học tốt!
HP
19 tháng 5 2021
a, Giả sử 6 số \(d_1,d_2,d_3,c_1,c_2,c_3\) mỗi số bằng 1 và -1, có tổng bằng 0 thì bắt buộc trong 6 số trên có ba số là 1 và ba số là -1
Vì \(d_1d_2d_3c_1c_2c_3=-1\Rightarrow\left(d_1d_2d_3\right)^2=-1\) \(\left(\text{vô lí}\right)\)
\(\Rightarrowđpcm\)