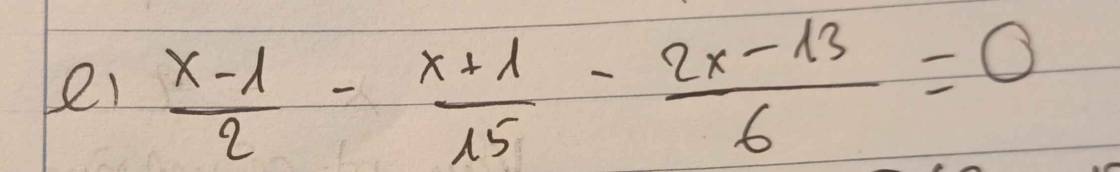 giải phương trình
giải phương trình
Đag cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
PT $\Leftrightarrow (4x^2+y^2-4xy)+9y^2+12x+6y+13=0$
$\Leftrightarrow (2x-y)^2+6(2x-y)+9y^2+12y+13=0$
$\Leftrightarrow (2x-y)^2+6(2x-y)+9+(9y^2+12y+4)=0$
$\Leftrightarrow (2x-y+3)^2+(3y+2)^2=0$
$\Rightarrow (2x-y+3)^2=(3y+2)^2=0$
$\Rightarrow y=-\frac{2}{3}; x=\frac{-11}{6}$

\(\left\{{}\begin{matrix}3x+y=8\left(1\right)\\2x-3y=1\left(2\right)\end{matrix}\right.\)
Từ (1) \(3x+y=8\Rightarrow y=8-3x\) (3)
Thế (3) vào (2):
\(2x-3\left(8-3x\right)=1\)
\(\Leftrightarrow11x=25\)
\(\Rightarrow x=\dfrac{25}{11}\)
Thế x vào (3) \(\Rightarrow y=8-\dfrac{3.25}{11}=\dfrac{13}{11}\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(\dfrac{25}{11};\dfrac{13}{11}\right)\)


Ta thấy : \(x^2+1\ge1\) nên để \(\left(3x-1\right)\left(x^2+1\right)< 0\)\(thì\) \(3x-1< 0\)\(hay\) \(x< \frac{1}{3}\)

$\begin{cases}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac16\\\dfrac{10}{3x}+\dfrac{10}{y}=1\\\end{cases}$
`<=>` $\begin{cases}\dfrac{10}{x}+\dfrac{10}{y}=\dfrac53\\\dfrac{10}{3x}+\dfrac{10}{y}=1\\\end{cases}$
`<=>` $\begin{cases}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac16\\\dfrac{20}{3}x=\dfrac23\\\end{cases}$
`<=>` $\begin{cases}x=\dfrac{1}{10}\\y=\dfrac{1}{15}\\\end{cases}$
Vậy `(x,y)=(1/10,1/15)`
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{10}{3x}+\dfrac{10}{y}=1\end{matrix}\right.\left(x,y\ne0\right)\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{10}{3}.\dfrac{1}{x}+10.\dfrac{1}{y}=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{10}{x}+\dfrac{10}{y}=\dfrac{5}{3}\left(1\right)\\\dfrac{10}{3}.\dfrac{1}{x}+\dfrac{10}{y}=1\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)-\left(2\right)\Rightarrow\dfrac{20}{3}.\dfrac{1}{x}=\dfrac{2}{3}\Rightarrow\dfrac{1}{x}=\dfrac{1}{10}\Rightarrow x=10\)
\(\Rightarrow\dfrac{1}{y}=\dfrac{1}{6}-\dfrac{1}{10}=\dfrac{1}{15}\Rightarrow y=15\)

lớp 9 ? mà ko làm dc bài này ?
\(x^2+2.14+196-128-196=0.\)
\(\left(x+14\right)^2-324=0\)
\(\left(x+14\right)^2-18^2=0\)
\(\hept{\begin{cases}\left(x+14+18\right)=0\\\left(x+14-18\right)=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-14-18\\x=-14+18\end{cases}}\)

a)
Khi m = 1, ta có:
{ x+2y=1+3
2x-3y=1
=> { x+2y=4
2x-3y=1
=> { 2x+4y=8
2x-3y=1
=> { x+2y=4
2x-3y-2x-4y=1-8
=> { x=4-2y
-7y = -7
=> { x = 2
y = 1
Vậy khi m = 1 thì hệ phương trình có cặp nghệm
(x; y) = (2;1)
a) Thay m=1 vào HPT ta có:
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+4y=8\\7y=7\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy HPT có nghiệm (x;y)= (2;1)

a) Thay m=1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7y=7\\x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=4-2y=4-2=2\end{matrix}\right.\)
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất là (x,y)=(2;1)
b) Ta có: \(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\2\left(m+3-2y\right)-3y=m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\2m+6-4y-3y-m=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\-7y+m+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\-7y=-m-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\y=\dfrac{m+6}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2\cdot\dfrac{m+6}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-\dfrac{2m+12}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7m+21-2m-12}{7}=\dfrac{5m+9}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x+y=3 thì \(\dfrac{5m+9}{7}+\dfrac{m+6}{7}=3\)
\(\Leftrightarrow6m+15=21\)
\(\Leftrightarrow6m=6\)
hay m=1
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất thỏa mãn x+y=3
a/ Thay \(m=1\) vào hpt ta có :
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy...
b/ Ta có :
\(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\\dfrac{2\left(m+3\right)}{2y}-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\\dfrac{m+3}{y}-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\m-3y^2+3=my\end{matrix}\right.\)

Đặt \(\dfrac{1}{x+1}\) = a; \(\dfrac{1}{y}\) = b (x \(\ne\) -1; y \(\ne\) 0)
Khi đó hpt trên tương đương:
\(\left\{{}\begin{matrix}a+b=\dfrac{-1}{2}\\8a+9b=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}8a+8b=-4\\8a+9b=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}-b=1\\8a+9b=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}b=-1\\8a+9\left(-1\right)=-5\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}b=-1\\8a=4\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}b=-1\\a=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}\dfrac{1}{x+1}=\dfrac{1}{2}\\\dfrac{1}{y}=-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x+1=2\\y=-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\) (TM)
Vậy hpt có nghiệm duy nhất (x; y) = (1; -1)
Chúc bn học tốt!
ĐK: ( x ≠ 1 ; y ≠ 0 )
Đặt a = \(\dfrac{1}{x+1} \) ; b = \(\dfrac{1}{y}\) . Ta có hệ phương trình
\(\begin{cases} a + b = \dfrac{-1}{2}\\ 8a + 9b = -5 \end{cases} \)
⇔\(\begin{cases} 8a + 8b = -4 \\ 8a + 9b = -5 \end{cases} \) ⇔ \(\begin{cases} -b = 1 \\ a + b = \dfrac{-1}{2} \end{cases} \) ⇔ \(\begin{cases} b = - 1 \\ a = \dfrac{1}{2} \end{cases} \)
=> \(\begin{cases} \dfrac{1}{y}=-1 \\\dfrac{1}{x+1}= \dfrac{1}{2} \end{cases} \) ⇔ \(\begin{cases} y = - 1\\ x = 1 \end{cases} \)
Vậy hpt có nghiệm duy nhất \(\begin{cases} y = - 1\\ x = 1 \end{cases} \)

\(x^4-10x^3+35x^2+24>0\)
\(\Leftrightarrow x^4-2.5.x^3+\left(5x\right)^2+10x^2+24>0\)
\(\Leftrightarrow\left(x^2-5x\right)^2+10x^2+24>0\)
\(\Leftrightarrow x^2\left(x-5\right)^2+10x^2+24>0\)(luôn đúng)
Vậy nghiệm của bất phương trình \(x\in R\)
\(\dfrac{x-1}{2}+\dfrac{x+1}{15}-\dfrac{2x-13}{6}=0\)
\(\Leftrightarrow\dfrac{15\left(x-1\right)}{30}-\dfrac{2\left(x+1\right)}{30}-\dfrac{5\left(2x-13\right)}{30}=0\)
\(\Leftrightarrow15\left(x-1\right)-2\left(x+1\right)-5\left(2x-13\right)=0\)
\(\Leftrightarrow15x-15-2x-2-10x+65=0\)
\(\Leftrightarrow3x+48=0\)
\(\Leftrightarrow x=-16\)