Tìm số dư trong phép chia \(14^{300}\) cho \(15\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ST
15 tháng 12 2021
Số dư \(234\) và đó là số dư lớn nhất có thể có được
\(\Rightarrow\) Số chia là : \(234+1=235\)
Thương là : \(15979:235=67\left(dư234\right)\)
15 tháng 12 2021
Số chia là \(234+1=235\)
Ta có \(15979:235=67R234\)
Vậy số chia là 235, thương là 67
5 tháng 1 2022
Số chia là 234+1=235
Ta có 15979:235=67R234
Vậy số chia là 235, thương là 67
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
5 tháng 1 2022
Số dư 234 và đó là số dư lớn nhất có thể => Số chia là: 235
(15979 - 234): 235= 67
=> Thương: 67
CM
7 tháng 6 2018
Số dư trong phép chia là số dư lớn nhất nên kém số chia 1 đơn vị.
Ta có sơ đồ sau:
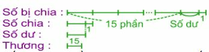
Theo sơ đồ, nếu gọi số chia là 1 phần, thêm 1 đơn vị vào số dư và số bị chia thì tổng số phần của số chia, số bị chia và số dư (mới) gồm : 15 + 1 + 1 + 1 = 18 (phần) như vậy. Khi đó tổng của số chia, số bị chia và số dư (mới) là : 769 - 15 + 1 + 1 = 756.
Số chia là : 756 : 18 = 42
Số dư là : 42 - 1 = 41
Số bị chia là : 42 x 15 + 41 = 671
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
17 tháng 1 2022
Số dư lớn nhất có giá trị nhỏ hơn số chia 1 đơn vị
số chia là
34+1=35
(15960-34):35 không chia hết => đề bài sai
HK
0
7 tháng 6 2015
Số chia cần tìm: (1423 + 1) : (15 + 1) = 89.
Số dư cần tìm: 89 – 1 = 88
KK
2
12 tháng 12 2019
Vì phép chia có số dư lớn nhất có thể mà số chia là 6
=> Số dư là 5
Vậy số bị chia là : 15 x6 +5 =95
9 tháng 6 2015
Số dư lớn nhất có thể là 6 vì số dư phải bé hơn số chia.
Số bị chia trong phép chia đó là : 15 x 7 +6 = 111
Đáp số : 111
28 tháng 10 2014
Số dư lớn nhất luôn kém số chia 1 đơn vị. Vậy số dư là:7-1=6
Số bị chia là:15*7+6=111
\(14\equiv-1\left(mod15\right)\Leftrightarrow14^{300}\equiv\left(-1\right)^{300}=1\left(mod15\right)\)
Vậy 14300 chia 15 dư 1