Cho tam giac ABC, tia phân giác góc B và C cắt nhau tại I. Chứng minh AI là tia phân giác góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 2 2021
Sửa đề: Phân giác góc B,C cắt nhau tại I
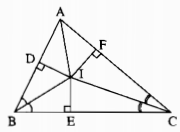
Kẻ ID⊥AB tại D, IF⊥AC tại F, IE⊥BC tại E
Xét ΔIDB vuông tại D và ΔIEB vuông tại E có
IB chung
\(\widehat{DBI}=\widehat{EBI}\)(BI là tia phân giác của \(\widehat{DBE}\))
Do đó: ΔIDB=ΔIEB(cạnh huyền-góc nhọn)
⇔ID=IE(hai cạnh tương ứng)(1)
Xét ΔIEC vuông tại E và ΔIFC vuông tại F có
IC chung
\(\widehat{ECI}=\widehat{FCI}\)(CI là tia phân giác của \(\widehat{ECF}\))
Do đó: ΔIEC=ΔIFC(cạnh huyền-góc nhọn)
⇒IE=IF(hai cạnh tương ứng)(2)
Từ (1) và (2) suy ra ID=IF(=IE)
Xét ΔADI vuông tại D và ΔAFI vuông tại F có
AI chung
ID=IF(cmt)
Do đó: ΔADI=ΔAFI(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{DAI}=\widehat{FAI}\)(hai góc tương ứng)
⇒\(\widehat{BAI}=\widehat{CAI}\)
mà tia AI nằm giữa hai tia AB,AC
nên AI là tia phân giác của \(\widehat{BAC}\)(đpcm)
11 tháng 5 2022
XétΔABC có
BI,CI là các tia phân giác
BI cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp
hay AI là tia phân giác của góc BAC
7 tháng 7 2023
Kẻ IK,IH,IE lần lượt vuông góc BC,AB,AC
Xét ΔBHI vuông tại H và ΔBKI vuông tại K có
BI chung
góc HBI=góc KBI
=>ΔBHI=ΔBKI
=>IH=IK
Xét ΔCKI vuông tại K và ΔCEI vuông tại E có
CI chung
góc KCI=góc ECI
=>ΔCKI=ΔCEI
=>IK=IE
=>IH=IE
Xét ΔAHI vuông tại H và ΔAEI vuông tại E có
AI chung
IH=IE
=>ΔAHI=ΔAEI
=>góc HAI=góc EAI
=>AI là phân giác của góc BAC
10 tháng 3 2022
Xét tam giác ABC vuông tại A:
BI; IC là đường phân giác (gt).
BI cắt CI tại I (gt).
\(\Rightarrow\) AI là tia phân giác góc BAC.
19 tháng 3 2022
Tam giác ABC có BI; CI là các đường phân giác giao nhau tại I
=> I là tâm đường tròn ngoại tiếp
=> AI là phân giác
Từ I hạ các đường vuông góc xuống 3 cạnh của tam giác. Bằng cách xét từng cặp tam giác vuông bằng nhau sẽ suy ra 3 đường vuông góc bằng nhau.
Sau đó xét trường hợp bằng nhau của cặp tam giác vuông chứ hai góc A1 và A2 theo trường hợp 2 tg vuông có cạnh huyền và 1 cạnh góc vuông băng nhau thì bằng nhau => A1=A2 => AI là phân giác ^A