Giải giúp tui bài 2 vs mn, mik đag cần gấp:((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Giúp mik bài 4 vs mn, mik đag cần gấp
MD
1
25 tháng 1
1: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)
Do đó: ΔFBH~ΔFAC
=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)
=>\(FB\cdot FC=FA\cdot FH\)
3: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
nên AEHD là tứ giác nội tiếp đường tròn đường kính AH
Tâm I là trung điểm của AH
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 1
a.
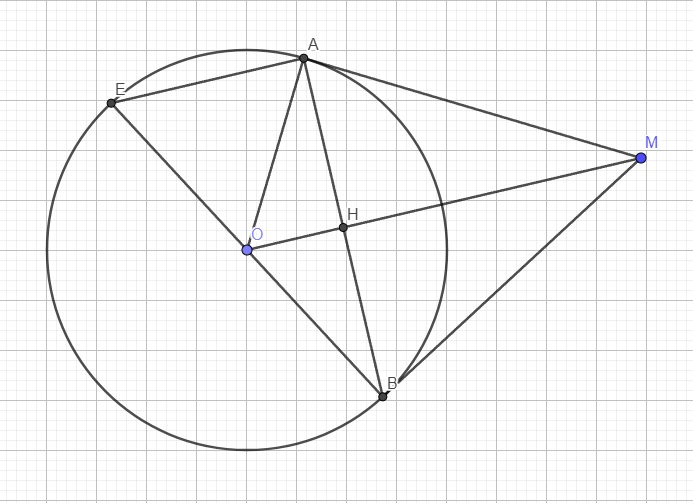
Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)
Xét hai tam giác OMA và OMB có:
\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)
\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)
\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến
b.
Gọi H là giao điểm AB và OM
Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H đồng thời \(HA=HB=\dfrac{AB}{2}\)
Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)
\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)
\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
Trong tam giác vuông OAH:
\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)
\(\Rightarrow AB=2AH=R\sqrt{3}\)
\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)
\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)
c.
BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)
Mà \(AB\perp OM\) (theo cm câu b)
\(\Rightarrow AE||OM\) (cùng vuông góc AB)
DL
0
25 tháng 11 2021
*Theo mình là
D.Cung cấp chất dinh dưỡng cho cây trồng
_______
𝗖𝗵𝘂́𝗰 𝗯𝗮̣𝗻 𝗱𝘁𝗵𝘄 𝗵𝗼̣𝗰 𝘁𝗼̂́𝘁( ◍•㉦•◍ )
🥺🍊
NN
mn giải giúp mik bài 1 và bài 2a với, mik đag cần gấp, mik cảm ơn mn nhiều
0
Bài 2:
1:
ĐKXĐ: x<>0
\(\dfrac{3x^3-4x^2+6x}{3x}\)
\(=\dfrac{3x^3}{3x}-\dfrac{4x^2}{3x}+\dfrac{6x}{3x}\)
\(=x^2-\dfrac{4}{3}x+2\)
2:
ĐKXĐ: x<>0
\(\dfrac{5x^4-3x^3+x^2}{3x^2}\)
\(=\dfrac{5x^4}{3x^2}-\dfrac{3x^3}{3x^2}+\dfrac{x^2}{3x^2}\)
\(=\dfrac{5}{3}x^2-x+\dfrac{1}{3}\)
3:
ĐKXĐ: x<>0
\(\dfrac{6x^5+4x^3-8x^2}{2x^2}\)
\(=\dfrac{6x^5}{2x^2}+\dfrac{4x^3}{2x^2}-\dfrac{8x^2}{2x^2}\)
\(=3x^3+2x-4\)
4:
ĐKXĐ: x<>0
\(\dfrac{-2x^5+3x^2-4x^3}{2x^2}\)
\(=-\dfrac{2x^5}{2x^2}+\dfrac{3x^2}{2x^2}-\dfrac{4x^3}{2x^2}\)
\(=-x^3+\dfrac{3}{2}-\dfrac{4}{3}x\)
5:
ĐKXĐ: x<>0
\(\dfrac{25x^5-5x^4+10x^2}{5x^2}\)
\(=\dfrac{25x^5}{5x^2}-\dfrac{5x^4}{5x^2}+\dfrac{10x^2}{5x^2}\)
\(=5x^3-x^2+2\)
6:
ĐKXĐ: x<>0
\(\dfrac{20x^6-5x^5+15x^4}{-3x^3}\)
\(=-\dfrac{20}{3}x^6:x^3+\dfrac{5x^5}{3x^3}-\dfrac{15x^4}{3x^3}\)
\(=-\dfrac{20}{3}x^3+\dfrac{5}{3}x^2-5x\)
7:
ĐKXĐ: x<>0
\(\dfrac{15x^7-25x^5+21x^3}{-5x^2}\)
\(=-\dfrac{15x^7}{5x^2}+\dfrac{25x^5}{5x^2}-\dfrac{21x^3}{5x^2}\)
\(=-3x^5+5x^3-\dfrac{21}{5}x\)
8:
ĐKXĐ: x<>0
\(\dfrac{-6x^8+14x^6-20x^4}{-4x^4}\)
\(=\dfrac{6x^8}{4x^4}-\dfrac{14x^6}{4x^4}+\dfrac{20x^4}{4x^4}\)
\(=\dfrac{3}{2}x^4-\dfrac{7}{2}x^2+5\)
9:
ĐKXĐ: x<>0
\(\dfrac{4x^5-3x^4+7x^2+6x}{-3x}\)
\(=-\dfrac{4x^5}{3x}+\dfrac{3x^4}{3x}-\dfrac{7x^2}{3x}-\dfrac{6x}{3x}\)
\(=-\dfrac{4}{3}x^4+x^3-\dfrac{7}{3}x-2\)
10:
ĐKXĐ: x<>0
\(\dfrac{-12x^6-7x^4-4x^3+2x^2}{-4x^2}\)
\(=\dfrac{12x^6}{4x^2}+\dfrac{7x^4}{4x^2}+\dfrac{4x^3}{4x^2}-\dfrac{2x^2}{4x^2}\)
\(=3x^4+\dfrac{7}{4}x^2+x-\dfrac{1}{2}\)