Cho điểm M nằm trong tam giác ABC. Chứng minh: MA + MB + MC < AB + AC + CB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
NT
1

14 tháng 4 2021
$M$ là điểm nằm trong $ΔABC$
nên ta có các tam giác $ΔMAB;MAC;MBC$
Xét $ΔMAB$ có: $MA+MB>AB$ (quan hệ giữa 3 cạnh trong 1 tam giác;bất đẳng thức tam giác)
tương tự $ΔMAC$ có: $MA+MC>AC$
$ΔMBC$ có: $MB+MC>BC$
nên $MA+MB+MA+MC+MB+MC>AB+BC+CA$
suy ra $2.(MA+MB+MC)>AB+BC+CA$
hay $MA+MB+MC>\dfrac{AB+BC+CA}{2}$
ND
0

MM
8

14 tháng 4 2020
Không làm mà đòi có ăn thì ............................................
14 tháng 4 2020
Nguôi ta de len day de giúp chu ko de cho may Súa nhe con .......
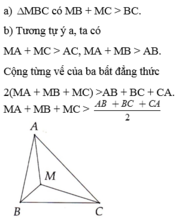
Kéo dài AM cắt BC tại A'.
Xét ΔABA' ta có BĐT: AB + BA' > AA' = MA + MA'
hay AB + BA' > MA + MA' (1)
Xét ΔCMA' ta có BĐT: CA' > MC - MA' (2) Cộng theo vế (1) và (2) ta được:
(AB + BA' ) + CA' > ( MA + MA' ) + ( MC - MA' ) <===> AB + (BA' + CA') > MA + MC
Hay: AB + CB > MA + MC (I) Chứng minh tương tự ta có:
AB + AC > MB + MC (II)
CB + AC > MA + MB (III) Cộng theo vế (I),(II) và (III) ta được:
2(AB+AC+CB) > 2(MA + MB + MC)
Hay: MA+MB+MC < AB+AC+CB (đpcm).