Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

$M$ là điểm nằm trong $ΔABC$
nên ta có các tam giác $ΔMAB;MAC;MBC$
Xét $ΔMAB$ có: $MA+MB>AB$ (quan hệ giữa 3 cạnh trong 1 tam giác;bất đẳng thức tam giác)
tương tự $ΔMAC$ có: $MA+MC>AC$
$ΔMBC$ có: $MB+MC>BC$
nên $MA+MB+MA+MC+MB+MC>AB+BC+CA$
suy ra $2.(MA+MB+MC)>AB+BC+CA$
hay $MA+MB+MC>\dfrac{AB+BC+CA}{2}$


Không làm mà đòi có ăn thì ............................................
Nguôi ta de len day de giúp chu ko de cho may Súa nhe con .......

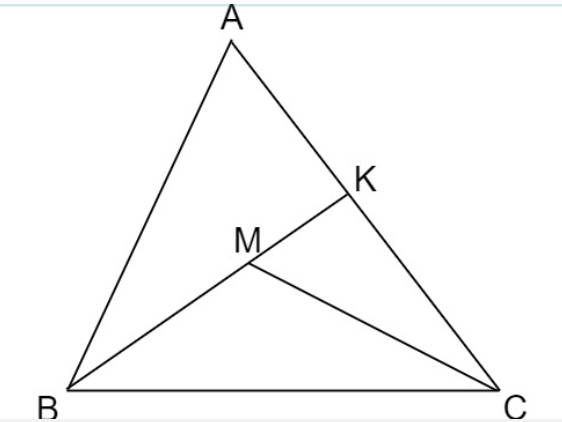
Kéo dài \(BM\) cắt \(AC\) tại \(K\)
Ta có: \(BK< AB+AK\) (bất đẳng thức t/g)
hay \(BM+MK< AB+AK\) \(\left(1\right)\)
Ta lại có: \(MC< MK+KC\) \(\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow BM+MK+MC< AB+AK+MK+KC\)
Hay \(BM+MC< AB+AK+KC\)
Hay \(BM+MC< AB+AC\)
https://lazi.vn/edu/exercise/757051/cho-tam-giac-abc-va-diem-m-nam-trong-tam-giac-chung-minh-rang-mb-mc-ab-ac
`->` Cop giỏi nhỉ?
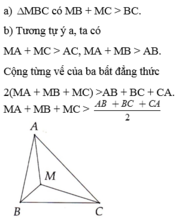
Kéo dài AM cắt BC tại A'.
Xét ΔABA' ta có BĐT: AB + BA' > AA' = MA + MA'
hay AB + BA' > MA + MA' (1)
Xét ΔCMA' ta có BĐT: CA' > MC - MA' (2) Cộng theo vế (1) và (2) ta được:
(AB + BA' ) + CA' > ( MA + MA' ) + ( MC - MA' ) <===> AB + (BA' + CA') > MA + MC
Hay: AB + CB > MA + MC (I) Chứng minh tương tự ta có:
AB + AC > MB + MC (II)
CB + AC > MA + MB (III) Cộng theo vế (I),(II) và (III) ta được:
2(AB+AC+CB) > 2(MA + MB + MC)
Hay: MA+MB+MC < AB+AC+CB (đpcm).