Cho a = log25, b = log35, c = log73. Hãy tính log14098 theo a, b, c.
Giúp mk vs ạ !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có: log 6 5 = 1 log 5 6 = 1 log 5 2 + log 5 3 = 1 1 a + 1 b = a b a + b

a) Ta có:
a = log 3 15 = log 3 ( 3 , 5 ) = log 3 3 + log 3 5 = 1 + log 3 5
Suy ra log 3 5 = a – 1
b = log 3 10 = log 3 ( 2 , 5 ) = log 3 2 + log 3 5
Suy ra log 3 2 = b − log 3 5 = b − (a − 1) = b – a + 1
Do đó:
log 3 50 = log 3 0 , 5 ( 2 . 52 ) = 2 log 3 2 + 4 log 3 5 = 2 (b – a + 1) + 4(a − 1) = 2a + 2b − 2
b) Ta có:
log 140 63 = log 140 ( 32 . 7 ) = 2 log 140 3 + log 140 7
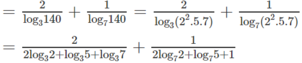
Từ đề bài suy ra:
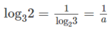
log 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
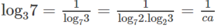
Vậy
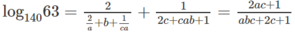

Ta có:
log 140 63 = log 140 3 2 . 7 = 2 log 140 3 + log 140 7
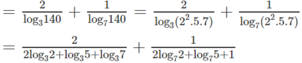
Từ đề bài suy ra:
![]()
loh 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
![]()
Vậy
![]()
\(log_{140}98=\dfrac{log_298}{log_2140}=\dfrac{log_2\left(2.7^2\right)}{log_2\left(2^2.5.7\right)}=\dfrac{log_22+2log_27}{2log_22+log_25+log_27}=\dfrac{1+2log_27}{2+a+log_27}\)
Ta có:
\(log_27=\dfrac{log_57}{log_52}=log_25.log_57=a.\left(\dfrac{log_37}{log_35}\right)=\dfrac{a}{log_35.log_73}=\dfrac{a}{bc}\)
\(\Rightarrow log_{140}98=\dfrac{1+\dfrac{2a}{bc}}{2+a+\dfrac{a}{bc}}=\dfrac{2a+bc}{a+2bc+abc}\)
có 28 viên bi đỏ,đổi 2 viên bi đỏ lấy 9 viên bi xanh,đổi 2 viên bi vàng.hỏi đổi được bao nhiêu viên bi vàng?