Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
log 140 63 = log 140 3 2 . 7 = 2 log 140 3 + log 140 7
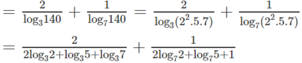
Từ đề bài suy ra:
![]()
loh 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
![]()
Vậy
![]()

a) Ta có:
a = log 3 15 = log 3 ( 3 , 5 ) = log 3 3 + log 3 5 = 1 + log 3 5
Suy ra log 3 5 = a – 1
b = log 3 10 = log 3 ( 2 , 5 ) = log 3 2 + log 3 5
Suy ra log 3 2 = b − log 3 5 = b − (a − 1) = b – a + 1
Do đó:
log 3 50 = log 3 0 , 5 ( 2 . 52 ) = 2 log 3 2 + 4 log 3 5 = 2 (b – a + 1) + 4(a − 1) = 2a + 2b − 2
b) Ta có:
log 140 63 = log 140 ( 32 . 7 ) = 2 log 140 3 + log 140 7
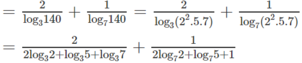
Từ đề bài suy ra:
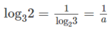
log 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
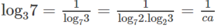
Vậy
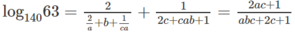

\(\frac{a^2}{b-1}+4\left(b-1\right)\ge4a\) ; \(\frac{b^2}{c-1}+4\left(c-1\right)\ge4b\); \(\frac{c^2}{a-1}+4\left(a-1\right)\ge4c\)
Cộng vế với vế, chuyển vế và rút gọn ta có đpcm
Dấu "=" xảy ra khi \(a=b=c=2\)

\(P=\dfrac{2-\left(1+a^2\right)}{1+a^2}+\dfrac{2-\left(1+b^2\right)}{1+b^2}+\dfrac{2}{\sqrt{1+c^2}}\)
\(P=2\left(\dfrac{1}{1+a^2}+\dfrac{1}{1+b^2}+\dfrac{1}{\sqrt{1+c^2}}\right)-2\)
Từ điều kiện \(ab+bc+ca=1\), đặt \(\left\{{}\begin{matrix}a=tanx\\b=tany\\c=tanz\end{matrix}\right.\) với \(x+y+z=\dfrac{\pi}{2}\)
Xét \(Q=\dfrac{1}{1+a^2}+\dfrac{1}{1+b^2}+\dfrac{1}{\sqrt{1+c^2}}=\dfrac{1}{1+tan^2x}+\dfrac{1}{1+tan^2y}+\dfrac{1}{\sqrt{1+tan^2z}}\)
\(Q=cos^2x+cos^2y+cosz=1+\dfrac{1}{2}\left(cos2x+cos2y\right)+cosz\)
\(=1+cos\left(x+y\right)cos\left(x-y\right)+cosz\le1+cos\left(x+y\right)+cosz\)
\(=1+cos\left(\dfrac{\pi}{2}-z\right)+cosz=1+sinz+cosz=1+\sqrt{2}sin\left(z+\dfrac{\pi}{4}\right)\le1+\sqrt{2}\)
\(\Rightarrow P\le2\left(1+\sqrt{2}\right)-2=2\sqrt{2}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x=y=\dfrac{\pi}{8}\\z=\dfrac{\pi}{4}\end{matrix}\right.\) \(\Rightarrow\left(a;b;c\right)=\left(\sqrt{2}-1;\sqrt{2}-1;1\right)\)
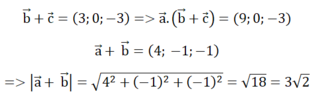
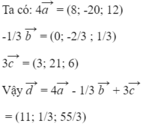
Chọn A.
Ta có:
Từ đề bài suy ra
Vậy