Cho nửa đường tròn tâm O, bán kính \(\frac{PQ}{2}\)ba điểm A, B, C nằm trên nửa đường tròn. CMR l\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)l > 1 biết PQ = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau \( \Leftrightarrow \) hai tia OA, OB đối nhau và OA = OB.
\( \Leftrightarrow \) O là trung điểm của AB hay AB là đường kính của đường tròn (O).
Vậy điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau là AB là đường kính của đường tròn (O).

Chắc đề là: \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\right|=a\) ?
\(\left|\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD}\right|=a\)
\(\Leftrightarrow\left|4\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right|=a\)
\(\Leftrightarrow4\left|\overrightarrow{MO}\right|=a\)
\(\Leftrightarrow MO=\dfrac{a}{4}\)
Tập hợp M là đường tròn tâm O bán kính \(\dfrac{a}{4}\)

Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được
 | = |
| = | |.cos(
|.cos( ,
, 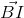 .
.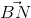 =
= 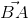 lý luận tương tự.
lý luận tương tự.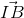 )
)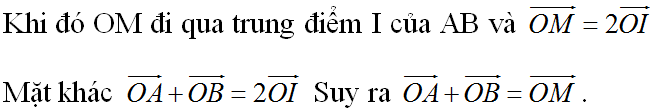
Trước tiên ta chứng minh với A, B, C là ba góc của 1 tam giác thì:
\(cos\left(2A\right)+cos\left(2B\right)+cos\left(2C\right)>-1\)
Ta có:
\(cos^2A+cos^2B+cos^2C=\frac{1+cos\left(2A\right)}{2}+\frac{1+cos\left(2B\right)}{2}+cos^2C\)
\(=1+\frac{cos\left(2A\right)+cos\left(2B\right)}{2}+cos^2C\)
\(=1+cos\left(A+B\right).cos\left(A-B\right)+cos^2C\)
\(=1-cos\left(C\right).cos\left(A-B\right)+cos^2C\)
\(=1-cos\left(C\right)\left(cos\left(A-B\right)-cosC\right)\)
\(=1-cos\left(C\right)\left(cos\left(A-B\right)-cos\left(A+B\right)\right)\)
\(=1-2cos\left(A\right).cos\left(B\right).cos\left(C\right)\)
Ta lại có:
\(-1\le cosA\le1;-1\le cosB\le1;-1\le cosC\le1\)
\(\Rightarrow cosA.cosB.cosC< 1\)
\(\Rightarrow cos\left(2A\right)+cos\left(2B\right)+cos\left(2C\right)=1-2cosA.cosB.cosC>1-2=-1\)
Quay lại bài toán ta có:
TH 1: Trong \(\overrightarrow{OA};\overrightarrow{OB};\overrightarrow{OC}\) có 2 vecto cùng phương ngược chiều giả sử là \(\overrightarrow{OA};\overrightarrow{OB}\) thì
\(\Rightarrow|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}|=|\overrightarrow{OC}|=OC=1\)
TH 2: Cả 3 vecto không cùng phương với nhau ta có ABC tạo thành tam giác.
\(|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}|^2=OA^2+OB^2+OC^2+2\left(\overrightarrow{OA}.\overrightarrow{OB}+\overrightarrow{OB}.\overrightarrow{OC}+\overrightarrow{OC}.\overrightarrow{OA}\right)\)
\(=3+2\left(cos\left(2A\right)+cos\left(2B\right)+cos\left(2C\right)\right)>3-2=1\)
Đâu = xảy ra khi trong ba vecto có 2 vecto cùng phương ngược chiều. Hay khi khi tam giác ABC là tam giác vuông.
Trước tiên ta chứng minh với A, B, C là ba góc của 1 tam giác thì:
cos(2A)+cos(2B)+cos(2C)>−1
Ta có:
cos2A+cos2B+cos2C=1+cos(2A)2 +1+cos(2B)2 +cos2C
=1+cos(2A)+cos(2B)2 +cos2C
=1+cos(A+B).cos(A−B)+cos2C
=1−cos(C).cos(A−B)+cos2C
=1−cos(C)(cos(A−B)−cosC)
=1−cos(C)(cos(A−B)−cos(A+B))
=1−2cos(A).cos(B).cos(C)
Ta lại có:
−1≤cosA≤1;−1≤cosB≤1;−1≤cosC≤1
⇒cosA.cosB.cosC<1
⇒cos(2A)+cos(2B)+cos(2C)=1−2cosA.cosB.cosC>1−2=−1
Quay lại bài toán ta có:
TH 1: Trong →OA;→OB;→OC có 2 vecto cùng phương ngược chiều giả sử là →OA;→OB thì
⇒|→OA+→OB+→OC|=|→OC|=OC=1
TH 2: Cả 3 vecto không cùng phương với nhau ta có ABC tạo thành tam giác.
|→OA+→OB+→OC|2=OA2+OB2+OC2+2(→OA.→OB+→OB.→OC+→OC.→OA)
=3+2(cos(2A)+cos(2B)+cos(2C))>3−2=1
Đâu = xảy ra khi trong ba vecto có 2 vecto cùng phương ngược chiều. Hay khi khi tam giác ABC là tam giác vuông.