giải pt:sinx+cos5x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
\(\Leftrightarrow cos5x=-sin3x\)
\(\Leftrightarrow cos5x=cos\left(\dfrac{\pi}{2}+3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}+3x+k2\pi\\5x=-\dfrac{\pi}{2}-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{16}+\dfrac{k\pi}{4}\end{matrix}\right.\)
GL
15 tháng 8 2017
1,Cho tam giác ABC gọi G là trọng tâm.Đường thẳng d không cắt tam giác ABC.Gọi A',B',C',G' lần lượt là hình chiếu của A,B,C,G trên đường thẳng d.Chứng minh rằng GG'=(AA'+BB'+CC')/3
CM
27 tháng 6 2018
sin3x - cos5x = 0
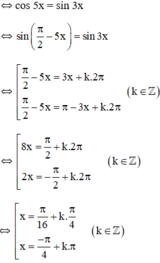
Vậy phương trình có hai họ nghiệm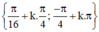 
(k ∈ Z).
NN
0
3 tháng 9 2020
nếu tính bình thường thì ra 2cos4x.cos(-x), sao nó lại mất dấu "-" vậy bạn?
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2020
\(\Leftrightarrow2cos4x.cosx+2cos^24x-1+1=0\)
\(\Leftrightarrow2cos4x\left(cos4x+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos4x+cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos4x=cos\left(\pi-x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\frac{\pi}{2}+k\pi\\4x=\pi-x+k2\pi\\4x=x-\pi+k2\pi\end{matrix}\right.\) \(\Leftrightarrow x=...\)
HP
12 tháng 7 2021
1.
\(2cos4x-3=0\)
\(\Leftrightarrow cos4x=\dfrac{3}{2}\)
Mà \(cos4x\in\left[-1;1\right]\)
\(\Rightarrow\) phương trình vô nghiệm.
2.
\(cos5x+2=0\)
\(\Leftrightarrow cos5x=-2\)
Mà \(cos5x\in\left[-1;1\right]\)
\(\Rightarrow\) phương trình vô nghiệm.
HP
12 tháng 7 2021
3.
\(cos2x+0,7=0\)
\(\Leftrightarrow cos2x=-\dfrac{7}{10}\)
\(\Leftrightarrow2x=\pm arccos\left(-\dfrac{7}{10}\right)+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{arccos\left(-\dfrac{7}{10}\right)}{2}+k\pi\)
4.
\(cos^22x-\dfrac{1}{4}=0\)
\(\Leftrightarrow cos^22x=\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-\dfrac{1}{2}\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\pm\dfrac{2\pi}{3}+k2\pi\\2x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k\pi\\x=\pm\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
PN
3