Question

[^($_DUY_$)^]

cho \(a^3+b^3+c^3=3abc\) và \(a+b+c\ne0\). C/M \(a=b=c\)

Answer 1

[Nguyễn Lê Phước Thịnh]

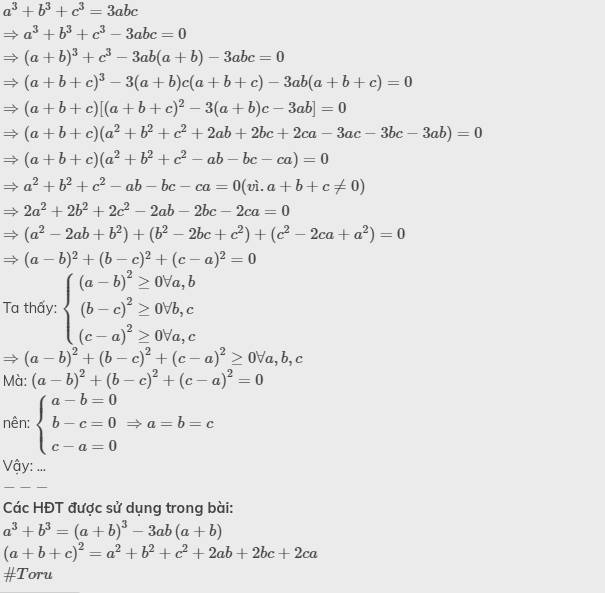
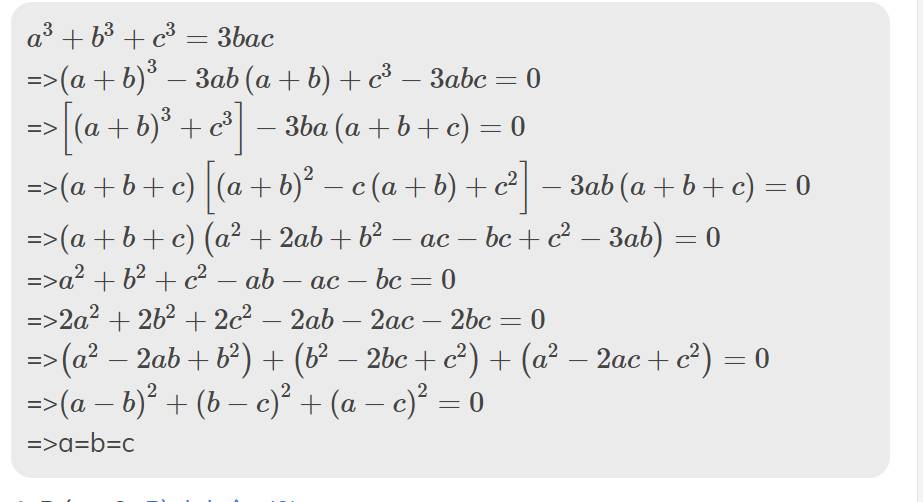
\(a^3+b^3+c^3=3bac\)

=>\(\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc=0\)

=>\(\left[\left(a+b\right)^3+c^3\right]-3ba\left(a+b+c\right)=0\)

=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)

=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)

=>\(a^2+b^2+c^2-ab-ac-bc=0\)

=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)

=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(a^2-2ac+c^2\right)=0\)

=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)

=>a=b=c

Answer 2

[Toru]

\(a^3+b^3+c^3=3abc\\\Rightarrow a^3+b^3+c^3-3abc=0\\\Rightarrow(a+b)^3+c^3-3ab(a+b)-3abc=0\\\Rightarrow (a+b+c)^3-3(a+b)c(a+b+c)-3ab(a+b+c)=0\\\Rightarrow(a+b+c)[(a+b+c)^2-3(a+b)c-3ab]=0\\\Rightarrow(a+b+c)(a^2+b^2+c^2+2ab+2bc+2ca-3ac-3bc-3ab)=0\\\Rightarrow(a+b+c)(a^2+b^2+c^2-ab-bc-ca)=0\\\Rightarrow a^2+b^2+c^2-ab-bc-ca=0(vì.a+b+c\ne0)\\\Rightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\\\Rightarrow(a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ca+a^2)=0\\\Rightarrow(a-b)^2+(b-c)^2+(c-a)^2=0\)

Ta thấy: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\forall a,b\\\left(b-c\right)^2\ge0\forall b,c\\\left(c-a\right)^2\ge0\forall a,c\end{matrix}\right.\)

\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\forall a,b,c\)

Mà: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)

nên: \(\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\Rightarrow a=b=c\)

Vậy: ...

\(---\)

Các HĐT được sử dụng trong bài:

\(a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\)

\(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ca\)

$\text{#}Toru$