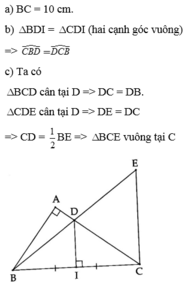
cho △ ABC vuông tại A , AB nhỏ hơn AC , lấy D là TĐ của AC . Trên tia đói của tia DB lấy điểm E sao cho DE = DB
a) CM △ADB=△CDE
b) Vẽ đường thẳng vuông góc với AC tại D , cắt BC tại K . CM AK=KC , CM góc ABK = góc KAB
c) trên tia KD lấy H sao cho D là TĐ của KH . CM K-H-E thẳng hàng ( vẽ hình)

a: Xét ΔADB và ΔCDE có
DA=DC
\(\widehat{ADB}=\widehat{CDE}\)(hai góc đối đỉnh)
DB=DE
Do đó: ΔADB=ΔCDE
b: Xét ΔKAC có
KD là đường cao
KD là đường trung tuyến
Do đó: ΔKAC cân tại K
=>KA=KC
Xét ΔABC có
D là trung điểm của AC
DK//AB
Do đó: K là trung điểm của CB
=>KC=KB
mà KC=KA
nên KA=KB
=>\(\widehat{KAB}=\widehat{KBA}\)
c:
Sửa đề: Chứng minh E,H,A thẳng hàng
Xét tứ giác AKCH có
D là trung điểm chung của AC và KH
=>AKCH là hình bình hành
=>AH//CK
mà K\(\in\)BC
nên AH//BC
Xét tứ giác BKHE có
D là trung điểm chung của BH và KE
=>BKHE là hình bình hành
=>BK//HE
mà K\(\in\)CB
nên HE//BC
Ta có: HE//BC
AH//BC
HE,AH có điểm chung là H
Do đó: A,E,H thẳng hàng