Bài 6. (0.5 điểm) Tìm cặp số nguyên $(x;y)$ thỏa mãn $x^2+x y+2 \, 023 x+2 \, 022 y+2 \, 023 = 0$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\Leftrightarrow y\left(x+1\right)-3\left(x+1\right)=5\\ \Leftrightarrow\left(x+1\right)\left(y-3\right)=5=5.1=\left(-5\right)\left(-1\right)\\ TH_1:\left\{{}\begin{matrix}x+1=1\\y-3=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=8\end{matrix}\right.\\ TH_2:\left\{{}\begin{matrix}x+1=5\\y-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=4\end{matrix}\right.\\ TH_3:\left\{{}\begin{matrix}x+1=-5\\y-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=2\end{matrix}\right.\\ TH_4:\left\{{}\begin{matrix}x+1=-1\\y-3=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{\left(0;8\right);\left(4;4\right);\left(-6;2\right);\left(-2;-2\right)\right\}\)
\(b,\Leftrightarrow6\left(n-1\right)+11⋮n-1\\ \Leftrightarrow n-1\in\left\{-11;-1;1;11\right\}\\ \Leftrightarrow n\in\left\{-10;0;2;12\right\}\)

Bài 1
a) (x + 3)(x + 2) = 0
x + 3 = 0 hoặc x + 2 = 0
*) x + 3 = 0
x = 0 - 3
x = -3 (nhận)
*) x + 2 = 0
x = 0 - 2
x = -2 (nhận)
Vậy x = -3; x = -2
b) (7 - x)³ = -8
(7 - x)³ = (-2)³
7 - x = -2
x = 7 + 2
x = 9 (nhận)
Vậy x = 9

Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
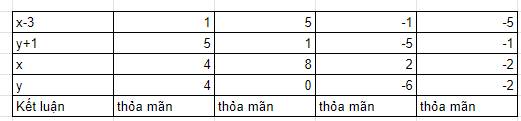
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.


Bài 1:
Thay \(x\) = 6y vào biểu thức ta có:
|6y| - |y| = 60
|5y| = 60
5.|y| = 60
|y| = 60 : 5
|y| = 12
\(\left[{}\begin{matrix}y=-12\\y=12\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=-72\\x=72\end{matrix}\right.\)
Kết luận:
Các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) = (-72; -12); (72; 12)

Bài 1 :
Phương trình <=> 2x . x2 = ( 3y + 1 ) 2 + 15
Vì \(\hept{\begin{cases}3y+1\equiv1\left(mod3\right)\\15\equiv0\left(mod3\right)\end{cases}\Rightarrow\left(3y+1\right)^2+15\equiv1\left(mod3\right)}\)
\(\Rightarrow2^x.x^2\equiv1\left(mod3\right)\Rightarrow x^2\equiv1\left(mod3\right)\)
( Vì số chính phương chia 3 dư 0 hoặc 1 )
\(\Rightarrow2^x\equiv1\left(mod3\right)\Rightarrow x\equiv2k\left(k\inℕ\right)\)
Vậy \(2^{2k}.\left(2k\right)^2-\left(3y+1\right)^2=15\Leftrightarrow\left(2^k.2.k-3y-1\right).\left(2^k.2k+3y+1\right)=15\)
Vì y ,k \(\inℕ\)nên 2k . 2k + 3y + 1 > 2k .2k - 3y-1>0
Vậy ta có các trường hợp:
\(+\hept{\begin{cases}2k.2k-3y-1=1\\2k.2k+3y+1=15\end{cases}\Leftrightarrow\hept{\begin{cases}2k.2k=8\\3y+1=7\end{cases}\Rightarrow}k\notinℕ\left(L\right)}\)
\(+,\hept{\begin{cases}2k.2k-3y-1=3\\2k.2k+3y+1=5\end{cases}\Leftrightarrow\hept{\begin{cases}2k.2k=4\\3y+1=1\end{cases}\Rightarrow}\hept{\begin{cases}k=1\\y=0\end{cases}\left(TM\right)}}\)
Vậy ( x ; y ) =( 2 ; 0 )
Bài 3:
Giả sử \(5^p-2^p=a^m\) \(\left(a;m\inℕ,a,m\ge2\right)\)
Với \(p=2\Rightarrow a^m=21\left(l\right)\)
Với \(p=3\Rightarrow a^m=117\left(l\right)\)
Với \(p>3\)nên p lẻ, ta có
\(5^p-2^p=3\left(5^{p-1}+2.5^{p-2}+...+2^{p-1}\right)\Rightarrow5^p-2^p=3^k\left(1\right)\) \(\left(k\inℕ,k\ge2\right)\)
Mà \(5\equiv2\left(mod3\right)\Rightarrow5^x.2^{p-1-x}\equiv2^{p-1}\left(mod3\right),x=\overline{1,p-1}\)
\(\Rightarrow5^{p-1}+2.5^{p-2}+...+2^{p-1}\equiv p.2^{p-1}\left(mod3\right)\)
Vì p và \(2^{p-1}\)không chia hết cho 3 nên \(5^{p-1}+2.5^{p-2}+...+2^{p-1}⋮̸3\)
Do đó: \(5^p-2^p\ne3^k\), mâu thuẫn với (1). Suy ra giả sử là điều vô lý
\(\rightarrowĐPCM\)

\(xy+3x-y=6\)
=> \(xy+3x-y-3=3\)
=> \(\left(xy+3x\right)-\left(y+3\right)=3\)
=> \(x\left(y+3\right)-\left(y+3\right)=3\)
=> \(\left(y+3\right)\left(x-1\right)=3\)
Mà x, y nguyên
=> \(x-1\)và \(y+3\)là số nguyên
=> \(\hept{\begin{cases}x-1=1\\y+3=3\end{cases}}\); \(\hept{\begin{cases}x-1=3\\y+3=1\end{cases}}\)và \(\hept{\begin{cases}x-1=-1\\y+3=-3\end{cases}}\)
=> \(\hept{\begin{cases}x=2\\y=0\end{cases}}\); \(\hept{\begin{cases}x=4\\y=-2\end{cases}}\)và \(\hept{\begin{cases}x=0\\y=-6\end{cases}}\)
Vậy cặp số nguyên (x;y) thỏa mãn là (2;0), (4;-2) và (0;-6)

Bài 2: Giả sử tồn tại x,y nguyên dương t/m đề, khi đó pt cho tương đương:
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x+3\right)^2+\left(2y+3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x+3=3\\2y+3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\y=0\end{cases}}\)
Vậy cặp nghiệm nguyên t/m pt là (x;y) = (0;0)
Làm lại bài 2 :v (P/S: Bạn bỏ bài kia đi nhé)
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x-3\right)^2+\left(2y-3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x-3=3\\2y-3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\y=3\end{cases}}\)
Vậy (x;y) = (3;3)
\(\Leftrightarrow x\left(x+y\right)+2022\left(x+y\right)+x+2023=0\)
\(\Leftrightarrow\left(x+y\right)\left(x+2022\right)+x+2022+1=0\)
\(\Leftrightarrow\left(x+2022\right)\left(x+y+1\right)=-1\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2022=1\\x+y+1=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x+2022=-1\\x+y+1=1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-2021\\y=2019\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2023\\y=2023\end{matrix}\right.\end{matrix}\right.\)