Cho (d):y=mx-2m+1 (m tham số)
1. Tìm m để (d)//(d') biết (d'):y=-x+3m
2. Tìm m để (d) cắt 2 trục Ox, Oy lần lượt ở A, B phân biệt thỏa mãn sinBAO = \(\dfrac{\sqrt{5}}{5}\), với O là gốc tọa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

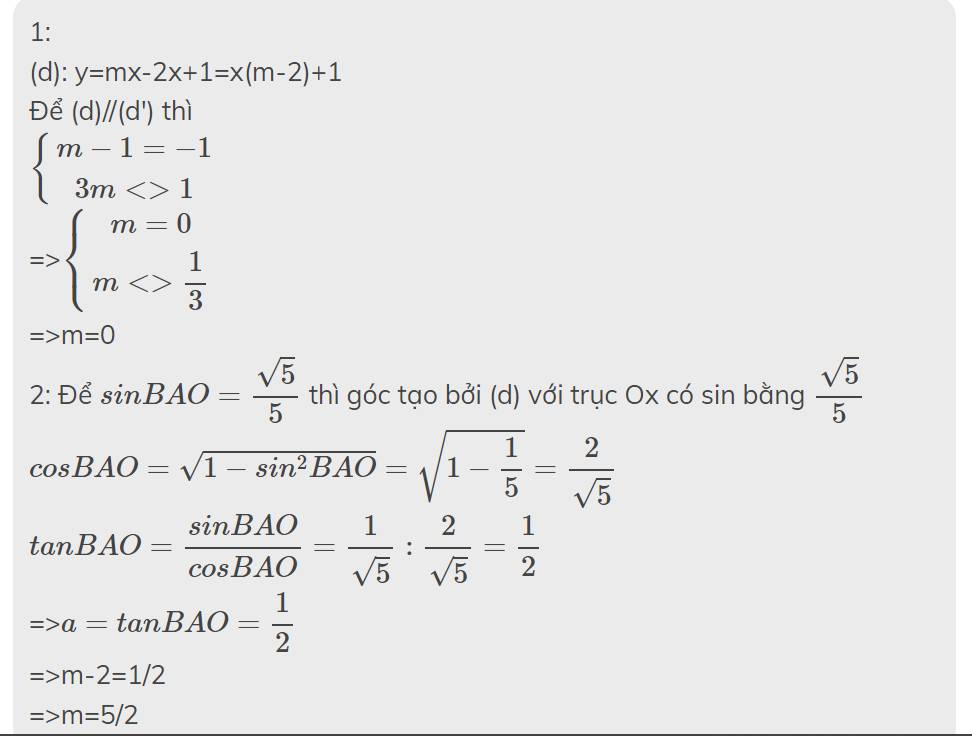

a: Khi m=1 thì (d): y=2x-1+2=2x+1
Khi m=1 thì (d'): y=-x-2
Phương trình hoành độ giao điểm là:
2x+1=-x-2
=>3x=-3
hay x=-1
=>y=-2+1=-1
b: Phương trình hoành độ giao điểm là:
\(2x-1+2m=-x-2m\)
=>3x-1+4m=0
=>3x=1-4m
=>x=(1-4m)/3
Để x dương thì 1-4m>0
hay m<1/4

1:
(d): y=mx-2x+1=x(m-2)+1
Để (d)//(d') thì
\(\left\{{}\begin{matrix}m-1=-1\\3m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=0\\m< >\dfrac{1}{3}\end{matrix}\right.\)
=>m=0
2: Để \(sinBAO=\dfrac{\sqrt{5}}{5}\) thì góc tạo bởi (d) với trục Ox có sin bằng \(\dfrac{\sqrt{5}}{5}\)
\(cosBAO=\sqrt{1-sin^2BAO}=\sqrt{1-\dfrac{1}{5}}=\dfrac{2}{\sqrt{5}}\)
\(tanBAO=\dfrac{sinBAO}{cosBAO}=\dfrac{1}{\sqrt{5}}:\dfrac{2}{\sqrt{5}}=\dfrac{1}{2}\)
=>\(a=tanBAO=\dfrac{1}{2}\)
=>m-2=1/2
=>m=5/2