Cho + = \frac{1}{a+b} ; ....
Đọc tiếp
Cho +
= \frac{1}{a+b} ;
. CMR
a)
b) +
=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2020
a/ \(\Leftrightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow x^2+y^2-2xy\ge0\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
b/ \(\frac{a}{a+b^2}=\frac{a}{a\left(a+b+c\right)+b^2}=\frac{a}{a^2+b^2+a\left(b+c\right)}\le\frac{a}{2ab+a\left(b+c\right)}=\frac{1}{b+b+b+c}\)
\(\Rightarrow\frac{a}{a+b^2}=\frac{1}{b+b+b+c}\le\frac{1}{16}\left(\frac{1}{b}+\frac{1}{b}+\frac{1}{b}+\frac{1}{c}\right)=\frac{1}{16}\left(\frac{3}{b}+\frac{1}{c}\right)\)
Tương tự: \(\frac{b}{b+c^2}\le\frac{1}{16}\left(\frac{3}{c}+\frac{1}{a}\right)\) ; \(\frac{c}{c+a^2}\le\frac{1}{16}\left(\frac{3}{a}+\frac{1}{c}\right)\)
Cộng vế với vế:
\(VT\le\frac{1}{16}\left(\frac{4}{a}+\frac{4}{b}+\frac{4}{c}\right)=\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Dấu "=" xảy ra khi \(a=b=c=\frac{1}{3}\)
T
13 tháng 2 2020
a) Áp dụng BĐT Cauchy-Schwarz dạng Engel: \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)
Tương tự:\(\frac{1}{b}+\frac{1}{c}\ge\frac{4}{b+c};\frac{1}{c}+\frac{1}{a}\ge\frac{4}{c+a}\)
Cộng theo vế 3 BĐT trên rồi chia cho 2 ta thu được đpcm
Đẳng thức xảy ra khi \(a=b=c\)
b)Đặt \(a+b=x;b+c=y;c+a=z\). Cần chứng minh:
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge2\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)\)
Cách làm tương tự câu a.
c) \(VT=\Sigma_{cyc}\frac{1}{\left(a+b\right)+\left(a+c\right)}\le\frac{1}{4}\Sigma_{cyc}\left(\frac{1}{a+b}+\frac{1}{a+c}\right)\le\frac{1}{16}\Sigma\left(\frac{2}{a}+\frac{1}{b}+\frac{1}{c}\right)=1\)
Đẳng thức xảy ra khi \(a=b=c=\frac{3}{4}\)
d) Em làm biếng quá anh làm nốt đi:P
13 tháng 5 2021
a)Áp dụng BĐT cosi-schwart:
`A=1/a+1/b+1/c>=9/(a+b+c)`
Mà `a+b+c<=3/2`
`=>A>=9:3/2=6`
Dấu "=" `<=>a=b=c=1/2`
b)Áp dụng BĐT cosi:
`a+1/(4a)>=1`
`b+1/(4b)>=1`
`c+1/(4c)>=1`
`=>a+b+c+1/(4a)+1/(4b)+1/(4c)>=3`
Ta có:
`1/a+1/b+1/c>=6`(Ở câu a)
`=>3/4(1/a+1/b+1/c)>=9/2`
`=>a+b+c+1/(a)+1/(b)+1/(c)>=3+9/2=15/2`
Dấu "=" `<=>a=b=c=1/2`
25 tháng 3 2022
a)Áp dụng BĐT cosi-schwart:
A=1a+1b+1c≥9a+b+cA=1a+1b+1c≥9a+b+c
Mà a+b+c≤32a+b+c≤32
⇒A≥9:32=6⇒A≥9:32=6
Dấu "=" ⇔a=b=c=12⇔a=b=c=12
b)Áp dụng BĐT cosi:
a+14a≥1a+14a≥1
b+14b≥1b+14b≥1
c+14c≥1c+14c≥1
⇒a+b+c+14a+14b+14c≥3⇒a+b+c+14a+14b+14c≥3
Ta có:
1a+1b+1c≥61a+1b+1c≥6(Ở câu a)
⇒34(1a+1b+1c)≥92⇒34(1a+1b+1c)≥92
⇒a+b+c+1a+1b+1c≥3+92=152⇒a+b+c+1a+1b+1c≥3+92=152
Dấu "=" ⇔a=b=c=12
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
Ta chứng minh BĐT sau với các số dương:
\(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)
Thật vậy, BĐT tương đương: \(\dfrac{x+y}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Áp dụng:
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\) ; \(\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{4}{b+c}\) ; \(\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{4}{c+a}\)
Cộng vế với vế:
\(2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge\dfrac{4}{a+b}+\dfrac{4}{b+c}+\dfrac{4}{c+a}\)
\(\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{2}{a+b}+\dfrac{2}{b+c}+\dfrac{2}{c+a}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
b.
Ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\Rightarrow\dfrac{3}{a}+\dfrac{3}{b}\ge\dfrac{12}{a+b}\) (1)
\(\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{4}{b+c}\Rightarrow\dfrac{2}{b}+\dfrac{2}{c}\ge\dfrac{8}{b+c}\) (2)
\(\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{4}{c+a}\) (3)
Cộng vế với vế (1); (2) và (3):
\(\dfrac{4}{a}+\dfrac{5}{b}+\dfrac{3}{c}\ge4\left(\dfrac{3}{a+b}+\dfrac{2}{b+c}+\dfrac{1}{c+a}\right)\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2019
a/ Đề sai, đề đúng phải là \(p=\frac{a+b+c}{2}\)
b/ \(\Leftrightarrow\frac{2}{2+a^2b}+\frac{2}{2+b^2c}+\frac{2}{2+c^2a}\ge2\)
\(VT=1-\frac{a^2b}{1+1+a^2b}+1-\frac{b^2c}{1+1+b^2c}+1-\frac{c^2a}{1+1+c^2a}\)
\(VT\ge3-\left(\frac{a^2b}{3\sqrt[3]{a^2b}}+\frac{b^2c}{3\sqrt[3]{b^2c}}+\frac{c^2a}{3\sqrt[3]{c^2a}}\right)\)
\(VT\ge3-\frac{1}{9}\left(3\sqrt[3]{a^2.ab.ab}+3\sqrt[3]{b^2.bc.bc}+3\sqrt[3]{c^2.ca.ca}\right)\)
\(VT\ge3-\frac{1}{9}\left(a^2+2ab+b^2+2bc+c^2+2ca\right)\)
\(VT\ge3-\frac{1}{9}\left(a+b+c\right)^2=2\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)
26 tháng 11 2020
Tự nhiên lục được cái này :'(
3. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\frac{1}{a+b-c}+\frac{1}{b+c-a}\ge\frac{\left(1+1\right)^2}{a+b-c+b+c-a}=\frac{4}{2b}=\frac{2}{b}\)
\(\frac{1}{b+c-a}+\frac{1}{c+a-b}\ge\frac{\left(1+1\right)^2}{b+c-a+c+a-b}=\frac{4}{2c}=\frac{2}{c}\)
\(\frac{1}{a+b-c}+\frac{1}{c+a-b}\ge\frac{\left(1+1\right)^2}{a+b-c+c+a-b}=\frac{4}{2a}=\frac{2}{a}\)
Cộng theo vế ta có điều phải chứng minh
Đẳng thức xảy ra <=> a = b = c
Cho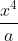
+ 
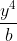= \frac{1}{a+b} ; 
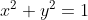. CMR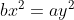
+ 
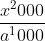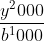= ^1000})
a)
b)
Cho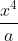
+ 
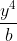= \frac{1}{a+b} ; 
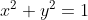. CMR
a)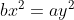
b)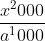
+ 
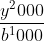= ^1000})
lưu ý chép kĩ nhé
nguyenchieubao
ai k cho mk thì mk cho lại