Bài 3.
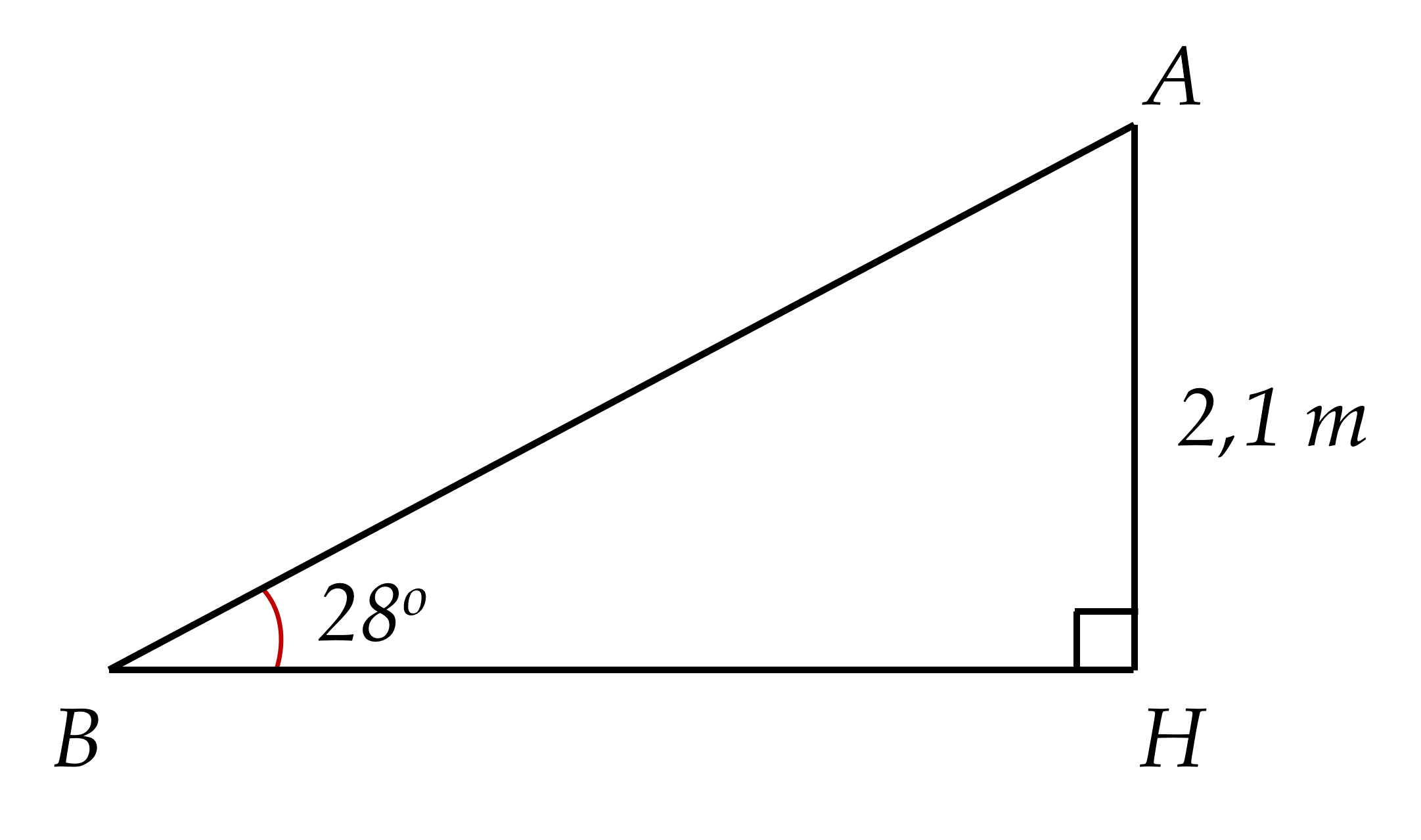
1) Một cầu trượt trong công viên có độ dốc so với mặt đất là $28^{\circ}$ và độ cao là $2,1$ m (được biểu diễn ở hình vẽ). Tính độ dài của mặt cầu trượt (kết quả làm tròn đến chữ số thập phân thứ nhất).
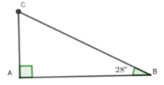
2) Cho đường tròn $(O ; R)$, đường kính $A B . M$ là điểm nằm trên đường tròn $(O ; R)$ và $A M<B M$ ( $M$ khác $A)$. Vẽ $O H$ vuông góc với $B M$ tại $H$. Tiếp tuyến tại $B$ của đường tròn $(O ; R)$ cắt $O H$ tại $N$.
a) Chứng minh $H$ là trung điểm của $B M$ và $M N$ là tiếp tuyến của đường tròn $(O ; R)$.
b) Gọi $K$ là trung điểm của $H N$. Gọi $I$ là giao điểm của $B K$ với $(O ; R)$. Chứng minh $\triangle M A B$ đồng dạng $\triangle H B N$ và ba điểm $A, H, I$ thẳng hàng.



nui
1) Xét △ABH vuông tại H có:
\(\sin\widehat{ABH}=\dfrac{AH}{AB}\)(tỉ số lượng giác)
⇒ \(AB=\dfrac{AH}{\sin\widehat{ABH}}=\dfrac{2,1}{\sin28^o}\approx4,5\left(m\right)\)
Vậy độ dài của mặt cầu trượt khoảng 4,5m.
2)
a) Xét △AMB có: A, M, B ∈ (O) (gt)
AB là đường kính của (O) (gt)
⇒ △AMB vuông tại M(ĐL về sự xác định của đường tròn)
Xét △AMB vuông tại M có: O là trung điểm AB(gt)
OH // AM (⊥ MB)
⇒ OH là đường trung bình của △AMB
⇒ H là trung điểm của MB (t/c)(đpcm)
Xét △NMB có: H là trung điểm của MB(cmt)
NH ⊥ MB(do N ∈ OH ⊥ MB)
⇒ NH là đường trung tuyến đồng thời cũng là đường cao trong △NMB
⇒ △NMB cân tại N(t/c △ cân)
⇒ NM = NB(t/c △ cân)
Xét △NMO và △NBO có:
ON chung
NM = NB(cmt)
OM = OB(= R)
⇒ △NMO = △NBO (c.c.c)
⇒ \(\widehat{NMO}=\widehat{NBO}=90^o\)
⇒ NM ⊥ MO
Mà OM = R
⇒ MN là tiếp tuyến của đường tròn (O; R) (đpcm)
b) Xét △MAB và △HBN có:
\(\widehat{AMB}=\widehat{BHN}=90^o\)
\(\widehat{MBA}=\widehat{HNB}\) (do cùng phụ với \(\widehat{NOB}\))
⇒ △MAB ∼ △HBN (g.g)(đpcm)