Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu c.
Gọi K là trung điểm của BH
Chỉ ra K là trực tâm của tam giác BMI
Chứng minh MK//EI
Chứng minh M là trung điểm của BE (t.c đường trung bình)


a, A,H,O thẳng hàng vì AH,AO cùng vuông góc với BC
HS tự chứng minh A,B,C,O cùng thuộc đường tròn đường kính OA
b, Ta có K D C ^ = A O D ^ (cùng phụ với góc O B C ^ )
=> ∆KDC:∆COA (g.g) => AC.CD = CK.AO
c, Ta có: M B A ^ = 90 0 - O B M ^ và M B C ^ = 90 0 - O M B ^
Mà O M B ^ = O B M ^ (∆OBM cân) => M B A ^ = M B C ^
=> MB là phân giác A B C ^ . Mặt khác AM là phân giác B A C ^
Từ đó suy ra M là tâm đường tròn nội tiếp tam giác ABC
d, Kẻ CD ∩ AC = P. Chứng minh ∆ACP cân tại A
=> CA = AB = AP => A là trung điểm CK

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

a) Nối O với N. Ta có \(\widehat{OAN}\)=\(\widehat{OBN}\)=\(\widehat{ONM}\)=90° →các góc này nội tiếp chắn nửa đường tròn đường kính ON →O,A,B,N,M cùng nằm trên đường tròn đường kính ON.
b) Nối A với M. Xét tứ giác nội tiếp OANB(chứng minhnội tiếp trước)ta có \(\widehat{AMO}\)=\(\frac{1}{2}\)\(\widebat{OA}\);\(\widehat{OAB}\)=\(\frac{1}{2}\)\(\widebat{OB}\) mà
- \(\widebat{OA}\)=\(\widebat{OB}\)→\(\widehat{AMO}\)=.\(\widehat{OAB}\)=\(\widehat{OAI}\)Xét tam giác OAI và tam giác OMA: \(\widehat{O}\)chung ,\(\widehat{OAI}\)=\(\widehat{AMO}\)\(\Rightarrow\)hai tam giác đồng dạng (g.g) \(\Rightarrow\)\(\frac{OI}{OA}\)=\(\frac{OA}{OM}\)\(\Leftrightarrow\)OI.OM=\(^{OA^2}\)=Rbình.
- c)

a: Ta có: ΔOBM cân tại O
mà OH là đường cao
nên H là trung điểm của BM và OH là phân giác của góc MOB
Xét ΔOBN và ΔOMN có
OB=OM
\(\widehat{BON}=\widehat{MON}\)
ON chung
Do đó: ΔOBN=ΔOMN
=>\(\widehat{OBN}=\widehat{OMN}=90^0\)
=>NM là tiếp tuyến của (O)
b: Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
Xét (O) có
\(\widehat{MAB}\) là góc nội tiếp chắn cung MB
\(\widehat{MBN}\) là góc tạo bởi tiếp tuyến BN và dây cung BM
Do đó: \(\widehat{MAB}=\widehat{MBN}\)
=>\(\widehat{MAB}=\widehat{HBN}\)
Xét ΔMAB vuông tại M và ΔHBN vuông tại H có
\(\widehat{MAB}=\widehat{HBN}\left(cmt\right)\)
Do đó: ΔMAB đồng dạng với ΔHBN
nui
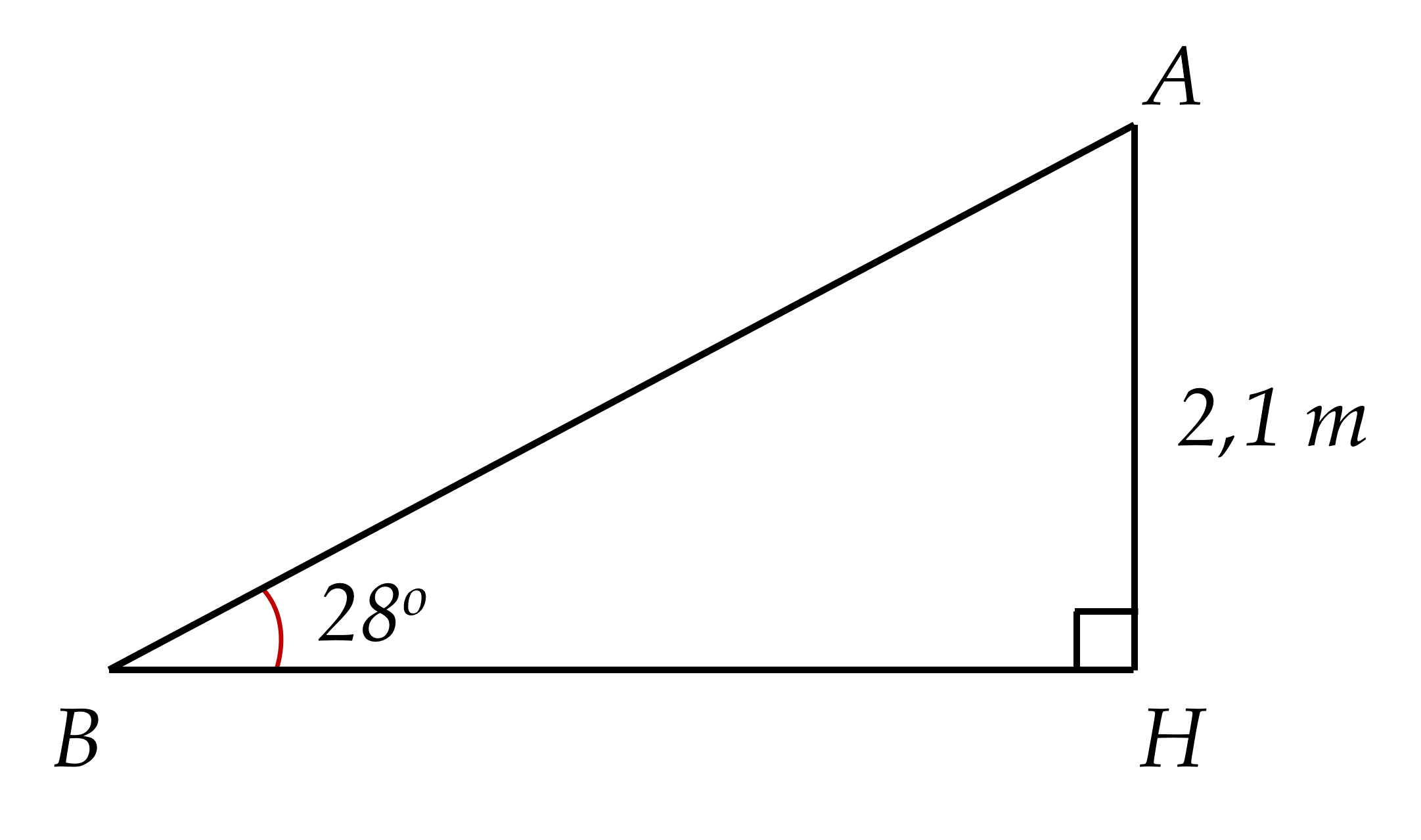
1) Xét △ABH vuông tại H có:
\(\sin\widehat{ABH}=\dfrac{AH}{AB}\)(tỉ số lượng giác)
⇒ \(AB=\dfrac{AH}{\sin\widehat{ABH}}=\dfrac{2,1}{\sin28^o}\approx4,5\left(m\right)\)
Vậy độ dài của mặt cầu trượt khoảng 4,5m.
2)
a) Xét △AMB có: A, M, B ∈ (O) (gt)
AB là đường kính của (O) (gt)
⇒ △AMB vuông tại M(ĐL về sự xác định của đường tròn)
Xét △AMB vuông tại M có: O là trung điểm AB(gt)
OH // AM (⊥ MB)
⇒ OH là đường trung bình của △AMB
⇒ H là trung điểm của MB (t/c)(đpcm)
Xét △NMB có: H là trung điểm của MB(cmt)
NH ⊥ MB(do N ∈ OH ⊥ MB)
⇒ NH là đường trung tuyến đồng thời cũng là đường cao trong △NMB
⇒ △NMB cân tại N(t/c △ cân)
⇒ NM = NB(t/c △ cân)
Xét △NMO và △NBO có:
ON chung
NM = NB(cmt)
OM = OB(= R)
⇒ △NMO = △NBO (c.c.c)
⇒ \(\widehat{NMO}=\widehat{NBO}=90^o\)
⇒ NM ⊥ MO
Mà OM = R
⇒ MN là tiếp tuyến của đường tròn (O; R) (đpcm)
b) Xét △MAB và △HBN có:
\(\widehat{AMB}=\widehat{BHN}=90^o\)
\(\widehat{MBA}=\widehat{HNB}\) (do cùng phụ với \(\widehat{NOB}\))
⇒ △MAB ∼ △HBN (g.g)(đpcm)