cho tam giác mnp, đừng cao me.gọi k,h lần lượt là hình chiếu của e trên mn,mp. m a) chứng minh mk.mn = mh.mp b.Biết me=h,góc M=en pha.Tính độ dài HK theo h và en pha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2021
2: Áp dụng hệ thức lượng trong tam giác vuông vào ΔMHN vuông tại H có HD là đường cao ứng với cạnh huyền MN, ta được:
\(MD\cdot MN=MH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔMHP vuông tại H có HE là đường cao ứng với cạnh huyền MP, ta được:
\(ME\cdot MP=MH^2\left(2\right)\)
Từ (1) và (2) suy ra \(MD\cdot MN=ME\cdot MP\)
CM
28 tháng 4 2018
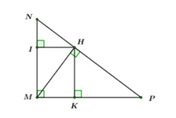
Xét tứ giác MIHK ta có M ^ = I ^ = K ^ = 90 0
=> MIHK là hình chữ nhật (dhnb)
=> HI = ML = 6cm
Áp dụng định lý Pytago cho MHK vuông tại K ta có:
Áp dụng hệ thức lượng trong MHP vuông tại H có đường cao HI ta có:
Áp dụng định lý Pytago cho MNP vuông tại N ta có:
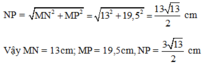
Đáp án cần chọn là: B
23 tháng 11 2023
a: Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot PH=MH^2\left(1\right)\)
Xét ΔNHM vuông tại H có HE là đường cao
nên \(ME\cdot MN=MH^2\left(2\right)\)
Từ (1) và (2) suy ra \(NH\cdot PH=ME\cdot MN\)
b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(\left\{{}\begin{matrix}MP^2=PH\cdot PN\\NM^2=NH\cdot NP\end{matrix}\right.\)
=>\(\dfrac{PH\cdot PN}{NH\cdot NP}=\dfrac{MP^2}{MN^2}\)
=>\(\dfrac{NH}{PH}=\left(\dfrac{MN}{MP}\right)^2\)
c: ΔMHP vuông tại H có HF là đường cao
nên \(MF\cdot MP=MH^2\)
mà \(ME\cdot MN=MH^2\)
nên \(MF\cdot MP=ME\cdot MN\)
=>\(\dfrac{MF}{ME}=\dfrac{MN}{MP}\)
Xét ΔMFN vuông tại M và ΔMEP vuông tại M có
\(\dfrac{MF}{ME}=\dfrac{MN}{MP}\)
Do đó: ΔMFN đồng dạng với ΔMEP
=>\(\widehat{MNF}=\widehat{MPE}\)
28 tháng 8 2023
a: ΔPIM vuông tại I
=>IP^2+IM^2=MP^2
=>IM^2=10^2-6^2=64
=>IM=8(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên PI*PN=PM^2
=>PN=10^2/6=50/3(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên MI^2=IN*IP
=>IN=8^2/6=32/3(cm)
Xét ΔMNP vuông tại M có sin MNP=MP/PN
=10:50/3=3/5
=>góc MNP=37 độ
b: C=MN+NP+MP
=10+40/3+50/3
=10+90/3
=10+30
=40(cm)
c: Xét ΔIMP vuông tại I có IK là đường cao
nên IK*PM=IP*IM
=>IK*10=6*8=48
=>IK=4,8(cm)
20 tháng 6 2023
a: Xét ΔHNM vuông tại H và ΔMNP vuôg tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: NP=căn 3^2+4^2=5cm
MH=3*4/5=2,4cm
NH=3^2/5=1,8cm
c; Đề bài yêu cầu gì?
17 tháng 4 2019
Em kham khảo link này nhé.
Câu hỏi của Đào Gia Khanh - Toán lớp 7 - Học toán với OnlineMath
a: Xét ΔMEN vuông tại E có EK là đường cao
nên \(MK\cdot MN=ME^2\left(1\right)\)
Xét ΔMEP vuông tại E có EH là đường cao
nên \(MH\cdot MP=ME^2\left(2\right)\)
Từ (1) và (2) suy ra \(MK\cdot MN=MH\cdot MP\)