Tìm x, y biết x^3-6y^3=xy(x-y)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


i) xy - 6y + 2x - 12
= (xy - 6y) + (2x - 12)
= y(x - 6) + 2(x - 6)
= (x - 6)(y + 2)
ii) 2x(y - z) + (z - y)(x + y)
= 2x(y - z) - (y - z)(x + y)
= (y - z)(2x - x - y)
= (y - z)(x - y)
b) x + 3 = (x + 3)2 ⇔ (x + 3)2 - (x + 3) = 0 ⇔ (x + 3)(x + 3 - 1) = 0
⇔ (x + 3)(x + 2) = 0
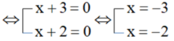
Vậy x = -3; x = -2
Tìm STN x,y biết:
a) (x + 5)(y - 3) =8
b) 2xy + y + 2x = 7
c) xy - 4x + 2y = 11
d) 3xy + x - 6y + 5 = 12


uuttqquuậậyy gửi từng bài thì có mà hết lượt gửi câu hỏi à

Đặt x/2=y/5=k
=>x=2k; y=5k
xy-15x+6y=40
\(\Leftrightarrow10k^2-15\cdot2k+6\cdot5k=40\)
\(\Leftrightarrow10k^2=40\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
=>x=4;y=10
TRường hợp 2: k=-2
=>x=-4; y=-10
Đặt `x/2 = y/5 = k`
`=>` `{(x = 2k),(y = 5k):}`
Ta có `: xy - 15x + 6y = 40`
`=> 2k . 5k - 15 . ( 2k ) + 6 . ( 5k ) = 40`
`=> 10k^2 - 30k + 30k = 40`
`=> k^2 = 40 : 10`
`=> k^2 = 4`
`=>` \(\left[ \begin{array}{l}k^2 = 2^2\\k^2 = ( - 2 )^2\end{array} \right.\)
`=>` \(\left[ \begin{array}{l}k = 2\\k = - 2\end{array} \right.\)
Xét `k = 2 => {(x = 2 . 2 = 4),(y = 5 . 2 = 10):}`
Xét `k = - 2 => {(x = - 2 . 2 = - 4),(y = - 2 . 5= - 10):}`
Vậy `, ( x ; y ) in { ( 4 ; 10 ) ; ( - 4 ; - 10 ) } .`

Bài 1:
\(x^2-8x+y^2+6y+25=0\)
\(\Leftrightarrow\)\(\left(x^2-8x+16\right)+\left(y^2+6y+9\right)=0\)
\(\Leftrightarrow\)\(\left(x-4\right)^2+\left(y+3\right)^2=0\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x-4=0\\y+3=0\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}x=4\\y=-3\end{cases}}\)
Vậy...
Bài 2:
Phương trình có nghiệm duy nhất là x = -2/3 nên ta có:
\(\left(4+a\right).\frac{-2}{3}=a-2\)
\(\Leftrightarrow\)\(-\frac{8}{3}-\frac{2}{3}a=a-2\)
\(\Leftrightarrow\)\(a+\frac{2}{3}a=2-\frac{8}{3}\)
\(\Leftrightarrow\)\(\frac{5}{3}a=-\frac{2}{3}\)
\(\Leftrightarrow\)\(a=-\frac{2}{5}\)
Bài 3:
\(A=a^4-2a^3+3a^2-4a+5\)
\(=a^3\left(a-1\right)-a^2\left(a-1\right)+2a\left(a-1\right)-2\left(a-1\right)+3\)
\(=\left(a-1\right)\left(a^3-a^2+2a-2\right)+3\)
\(=\left(a-1\right)\left[a^2\left(a-1\right)+2\left(a-1\right)\right]+3\)
\(=\left(a-1\right)^2\left(a^2+2\right)+3\ge3\)
\(\text{Vậy Min A=3. Dấu "=" xảy ra khi và chỉ khi }a-1=0\Leftrightarrow a=1\)
Bài 4:
\(xy-3x+2y=13\)
\(\Leftrightarrow x\left(y-3\right)+2\left(y-3\right)=7\)
\(\Leftrightarrow\left(x+2\right)\left(y-3\right)=7=1.7=7.1=-1.-7=-7.-1\)
| x+2 | -7 | -1 | 1 | 7 |
| y-3 | -1 | -7 | 7 | 1 |
| x | -9 | -3 | -1 | 5 |
| y | 2 | -4 | 10 | 4 |
Vậy...
Bài 5:
\(xy-x-3y=2\)
\(\Leftrightarrow x\left(y-1\right)-3\left(y-1\right)=5\)
\(\Leftrightarrow\left(x-3\right)\left(y-1\right)=5=1.5=5.1=-1.-5=-5.-1\)
| x-3 | -5 | -1 | 1 | 5 |
| y-1 | -1 | -5 | 5 | 1 |
| x | -2 | 2 | 4 | 8 |
| y | 0 | -4 | 6 | 2 |
Vậy....
Lời giải:
Nếu $x=0$ thì: $0-6y^3=0\Rightarrow y=0$
Nếu $x\neq 0$. Đặt $y=tx$. Khi đó
PT $\Leftrightarrow x^3-6x^3t^3=x.tx(x-tx)$
$\Leftrightarrow x^3(1-6t^3)=x^3t(1-t)$
$\Leftrightarrow x^3[(1-6t^3)-t(1-t)]=0$
$\Leftrightarrow 1-6t^3-t+t^2=0$ (do $x\neq 0$)
$\Leftrightarrow 6t^3-t^2+t-1=0$
$\Leftrightarrow (2t-1)(3t^2+t+1)=0$
$\Leftrightarrow 2t-1=0$ hoặc $3t^2+t+1=0$
Dễ thấy $3t^2+t+1>0$ với mọi $t\in\mathbb{R}$
$\Rightarrow 2t-1=0\Leftrightarrow t=\frac{1}{2}$
Vậy $x=2y$. Đến đây bạn thay vào pt ban đầu để tìm $x,y$.