Cho f(x)=\(\dfrac{x^2-1}{x}\) .Tính f(n)(x) với n≥2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{1+\dfrac{1}{x^2}+\dfrac{1}{\left(x+1\right)^2}}=\sqrt{\dfrac{x^2+\left(x+1\right)^2+x^2\left(x+1\right)^2}{x^2\left(x+1\right)^2}}=\sqrt{\dfrac{x^2\left(x+1\right)^2+2x^2+2x+1}{x^2\left(x+1\right)^2}}\)
\(=\sqrt{\dfrac{\left(x^2+x\right)^2+2\left(x^2+x\right)+1}{\left(x^2+x\right)^2}}=\sqrt{\dfrac{\left(x^2+x+1\right)^2}{\left(x^2+x\right)^2}}=\dfrac{x^2+x+1}{x^2+x}\)
\(=1+\dfrac{1}{x}-\dfrac{1}{x+1}\)
\(\Rightarrow f\left(1\right).f\left(2\right)...f\left(2020\right)=5^{1+1-\dfrac{1}{2}+1+\dfrac{1}{2}-\dfrac{1}{3}+...+1+\dfrac{1}{2020}-\dfrac{1}{2021}}\)
\(=5^{2021-\dfrac{1}{2021}}\)
\(\Rightarrow\dfrac{m}{n}=2021-\dfrac{1}{2021}=\dfrac{2021^2-1}{2021}\)
\(\Rightarrow m-n^2=2021^2-1-2021^2=-1\)

\(a,F=\dfrac{x^2+x+4x^2+2-x^2+3x-2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x}{x-1}\\ b,\left|x+2\right|=1\Leftrightarrow\left[{}\begin{matrix}x=1-2=-1\left(ktm\right)\\x=-1-2=-3\end{matrix}\right.\Leftrightarrow x=-3\\ \Leftrightarrow F=\dfrac{-12}{-4}=3\\ c,K=F\left(x-1\right)-x^2-2021=4x-x^2-2021\\ K=-\left(x^2-4x+4\right)-2017=-\left(x-2\right)^2-2017\le-2017\\ K_{max}=-2017\Leftrightarrow x=2\left(tm\right)\)

b/ Theo đề bài thì ta có:
\(\left\{{}\begin{matrix}f\left(1\right)=f\left(-1\right)\\f\left(2\right)=f\left(-2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a_4+a_3+a_2+a_1+a_0=a_4-a_3+a_2-a_1+a_0\\16a_4+8a_3+4a_2+2a_1+a_0=16a_4-8a_3+4a_2-2a_1+a_0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a_3+a_1=0\\4a_3+a_1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a_3=0\\a_1=0\end{matrix}\right.\)
Ta có: \(f\left(x\right)-f\left(-x\right)=a_4x^4+a_3x^3+a_2x^2+a_1x+a_0-\left(a_4x^4-a_3x^3+a_2x^2-a_1x+a_0\right)\)
\(=2a_3x^3+2a_1x=0\)
Vậy \(f\left(x\right)=f\left(-x\right)\)với mọi x
a/ Áp dụng tính chất dãy tỷ số bằng nhau ta có:
\(\dfrac{a}{2015}=\dfrac{b}{2016}=\dfrac{c}{2017}=\dfrac{a-b}{-1}=\dfrac{b-c}{-1}=\dfrac{c-a}{2}\)
\(\Rightarrow c-a=-2\left(a-b\right)=-2\left(b-c\right)\)
Thế vào B ta được
\(B=4\left(a-b\right)\left(b-c\right)-\left(c-a\right)^2\)
\(=4\left(a-b\right)\left(b-c\right)-\left[-2\left(a-b\right).\left(-2\right).\left(b-c\right)\right]\)
\(=4\left(a-b\right)\left(b-c\right)-4\left(a-b\right)\left(b-c\right)=0\)

Câu a thì dài, câu b thì ngắn. Xin giải câu b trước để đi ngủ
b) Giải:
Vì \(f\left(x_1.x_2\right)=f\left(x_1\right).f\left(x_2\right)\) nên:
\(f\left(4\right)=f\left(2.2\right)=f\left(2\right).f\left(2\right)=10.10=100\)
\(f\left(16\right)=f\left(4.4\right)=f\left(4\right).f\left(4\right)=100.100=10000\)
\(f\left(32\right)=f\left(16.2\right)=f\left(16\right).f\left(2\right)=10000.10=100000\)
Vậy \(f\left(32\right)=100000\)

Phần này khó chú ý nè bạn
Giải
Ta có f(x1+x2) = f(x1) + f(x2)
nên f(7) = f(3)+f(4)= f(2)+f(1) + f(2)+f(2) = f(1)+f(1)+f(1)+f(1)+f(1)+f(1)+f(1)=7
\(f\left(\dfrac{1}{7}\right)=\dfrac{1}{49}.f\left(7\right)=\dfrac{1}{49}.7=\dfrac{1}{7}\)
Ta có :\(f\left(\dfrac{5}{7}\right)=f\left(\dfrac{2}{7}\right)+f\left(\dfrac{3}{7}\right)=f\left(\dfrac{1}{7}\right)+f\left(\dfrac{1}{7}\right)+f\left(\dfrac{1}{7}\right)+f\left(\dfrac{2}{7}\right)=f\left(\dfrac{1}{7}\right)+f\left(\dfrac{1}{7}\right)+f\left(\dfrac{1}{7}\right)+f\left(\dfrac{1}{7}\right)+f\left(\dfrac{1}{7}\right)=\dfrac{1}{7}+\dfrac{1}{7}+\dfrac{1}{7}+\dfrac{1}{7}+\dfrac{1}{7}=\dfrac{5}{7}\)
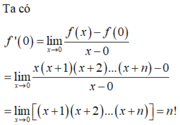

\(f\left(x\right)=x-\dfrac{1}{x}\Rightarrow f'\left(x\right)=1+\dfrac{1}{x^2}\); \(f''\left(x\right)=-\dfrac{2}{x^3}=\dfrac{\left(-1\right)^{2-1}.2!}{x^{2+1}}\) ;
\(f^{\left(3\right)}\left(x\right)=\dfrac{6}{x^4}=\dfrac{\left(-1\right)^{3-1}.3!}{x^{3+1}}\)
\(\Rightarrow f^{\left(n\right)}\left(x\right)=\dfrac{\left(-1\right)^{n-1}.n!}{x^{n+1}}\)