Bài 3 (3 điểm)
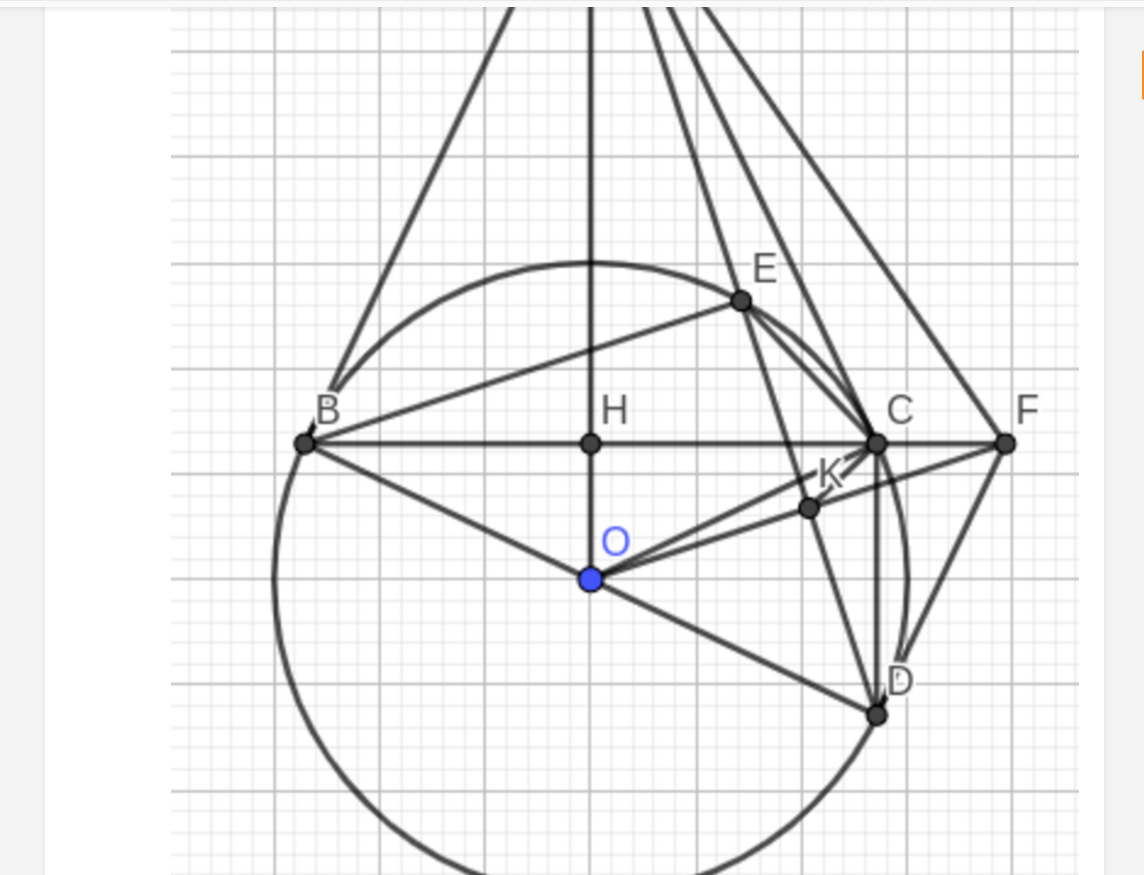
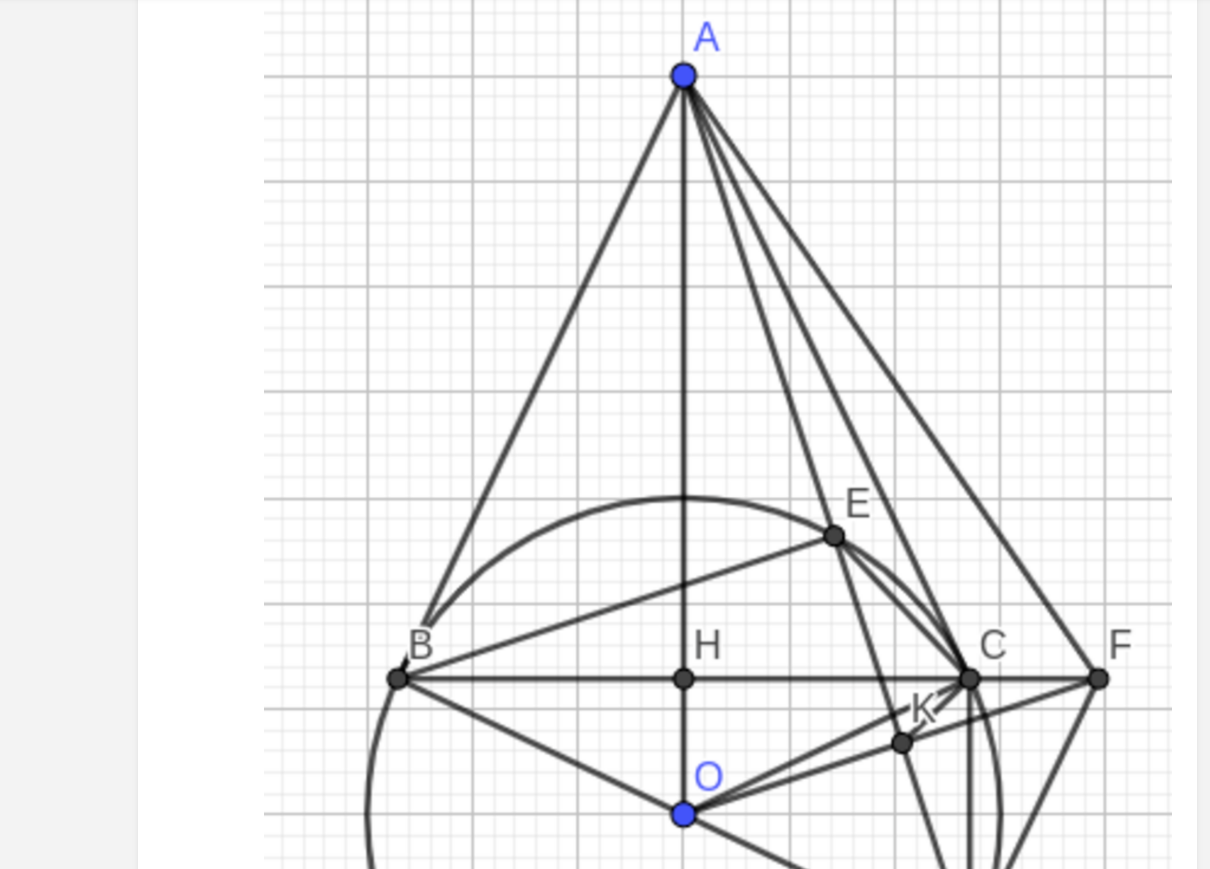
1) Cho đường tròn $(O)$ và một điểm $P$ nằm ngoài đường tròn $(O)$. Từ $P$ vẽ hai tiếp tuyến $PA$, $PB$ của đường tròn $(O)$ ($A$ và $B$ là hai tiếp điểm tiếp điểm). Gọi $H$ là giao điểm của $OP$ và $AB$.
a) Chứng minh $OP$ vuông góc với $AB$ tại $H$.
b) Từ $A$ vẽ đường kính $AD$ của $(O)$, đường thẳng $PD$ cắt $(O)$ tại $E$ (khác $D$). Chứng minh: $PD.PE = PH.PO$.
2) Chiều rộng của sân bóng đá và của khung thành là $AB = 64,32$ m, $KT = 7,32$ m và $AK = TB$.
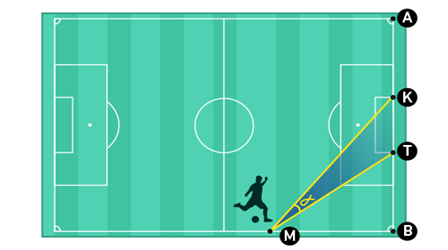
Một cầu thủ điều khiển bóng tấn công dọc theo đường biên và sút bóng tại vị trí $M$ cách $B$ một khoảng $35$ m. Tính góc sút $\alpha $ khi bóng đi trúng khung thành $KT$ (làm tròn đến độ).