Cho A = 4+4^2+4^3+...+4^23+4^24
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 1 2018
a = 4 + 42 + 43 + ... + 424
=> 2a = 42 + 43 + 44 + .... + 425
=> a = ( 42 + 43 + 44 + .... + 425 ) - ( 4 + 42 + 43 + ... + 424 )
=> a = 425 - 4
Vậy a = 425 - 4
DH
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 12 2023
a/
\(A=\left(4+4^2\right)+4^2\left(4+4^2\right)+...+4^{22}\left(4+4^2\right)=\)
\(=20\left(1+4^2+4^4+...+4^{22}\right)⋮20\)
b/
\(A=\left(4+4^2+4^3\right)+...+\left(4^{22}+4^{23}+4^{24}\right)=\)
\(=4\left(1+4+4^2\right)+...+4^{22}\left(1+4+4^2\right)=\)
\(=21\left(4+4^4+...+4^{22}\right)⋮21\)
c/
A đồng thời chia hết cho 20 và 21, mà 20 và 21 là 2 số nguyên tố cùng nhau
\(\Rightarrow A⋮20.21=420\)
HM
1
12 tháng 8 2019
A=4+4^2+4^3+...+4^24
A=(4 + 4^2)+(4^3 + 4^4)+...+(4^23 + 4^24)
A=20.(1+4^4+...+4^24)chia hết cho 20
DT
1
AH
Akai Haruma
Giáo viên
29 tháng 12 2023
Lời giải:
$A=(4+4^2)+(4^3+4^4)+....+(4^{23}+4^{24})$
$=(4+4^2)+4^2(4+4^2)+....+4^{22}(4+4^2)$
$=(4+4^2)(1+4^2+...+4^{22})$
$=20(1+4^2+...+4^{22})\vdots 20$
----------------------------
$A=(4+4^2+4^3)+(4^4+4^5+4^6)+....+(4^{22}+4^{23}+4^{24})$
$=4(1+4+4^2)+4^4(1+4+4^2)+....+4^{22}(1+4+4^2)$
$=(1+4+4^2)(4+4^4+...+4^{22})$
$=21(4+4^4+....+4^{22})\vdots 21$
----------------------
Vậy $A\vdots 20; A\vdots 21$. Mà $(20,21)=1$ nên $A\vdots (20.21)$ hay $A\vdots 420$
D
0
AP
3
KV
20 tháng 12 2023
A = 4 + 4² + 4³ + ... + 4²³ + 4²⁴
Số số hạng của A:
24 - 1 + 1 = 24
Do 24 ⋮ 2 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 2 số hạng như sau:
A = (4 + 4²) + (4³ + 4⁴) + ... + (4²³ + 4²⁴)
= 20 + 4².(4 + 4²) + ... + 4²².(4 + 4²)
= 20 + 4².20 + ... + 4²².20
= 20.(1 + 4² + ... + 4²²) ⋮ 20
Vậy A⋮ 20 (1)
Do 24 ⋮ 3 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 3 số hạng như sau:
A = (4 + 4² + 4³) + (4⁴ + 4⁵ + 4⁶) + ... + (4²² + 4²³ + 4²⁴)
= 4.(1 + 4 + 4²) + 4⁴.(1 + 4 + 4²) + ... + 4²².(1 + 4 + 4²)
= 4.21 + 4⁴.21 + ... + 4²².21
= 21.(4 + 4⁴ + ... + 4²²) ⋮ 21
Vậy A ⋮ 21 (2)
Từ (1) và (2) ⇒ A ⋮ 20 . 21 (do 20 và 21 nguyên tố cùng nhau)
⇒ A ⋮ 420
Vậy A chia hết cho 20; 21; 420
BT
6
MH
13 tháng 7 2017
A = \(4+4^2+4^3+.....+4^{23}+4^{24}\)
= \(4\left(1+4+4^2\right)+.....+4^{22}+\left(1+4+4^2\right)\)
= \(4.21+.....+4^{22}.21\)
= \(21\left(4+...+4^{22}\right)⋮21\)
Vậy A chia hết cho 21
Ai k mik mik k lại nha
HC
13 tháng 7 2017
Lâu r chị k nhớ lắm nhé
CM A chia hết cho 20
A = 4(1+4+4^2+...+4^23) chia hết cho 4 (1)
A = (4+4^2) + (4^3+4^4) + ...+ (4^23+4^24)
= 4(1+4) + 4^3(1+4) +...+4^23(1+4)
= (1+4)(4+4^3+4^5+...+4^23)
=5.(4+4^3+4^5+...+4^23) chia hết cho 5 (2)
Mà UCLN(4,5)=1 (3)
Vậy A chia hết cho 4.5 =20
CM A chia hết cho 21
A = (4+4^2+4^3)+(4^4+4^5+4^6)+...+(4^22+4^23+4^24)
= 4(1+4+4^2) +4^4(1+4+4^2)+...+4^22(1+4+4^2)
= (1+4+4^2)(4+4^4+...+4^22)
= 21(4+4^4+...+4^22) chia hết cho 21
Vậy A chia hết cho 24.
Chúc e học giỏi!
PT
4
12 tháng 4 2017
A = 4+42+43+...+424 ( Có 24 số hạng )
A = (4+42) + (43+44) + ... + (423+424) ( Có 12 cặp )
A = 20 + 42.(4+42) + ... + 422.(4+42)
A = 20 + 42.20 + ... + 422.20 \(⋮\)20
\(\Rightarrow\)A \(⋮\)20 (đpcm)
12 tháng 4 2017
Đặt A= 4+42+43+...+423+424
=> 4A= 42+43+44+...+424+425
=> 4A-A = 425 - 4
=> 3A = 425 - 4
=> A = ( 425 - 4) : 3
TH
1
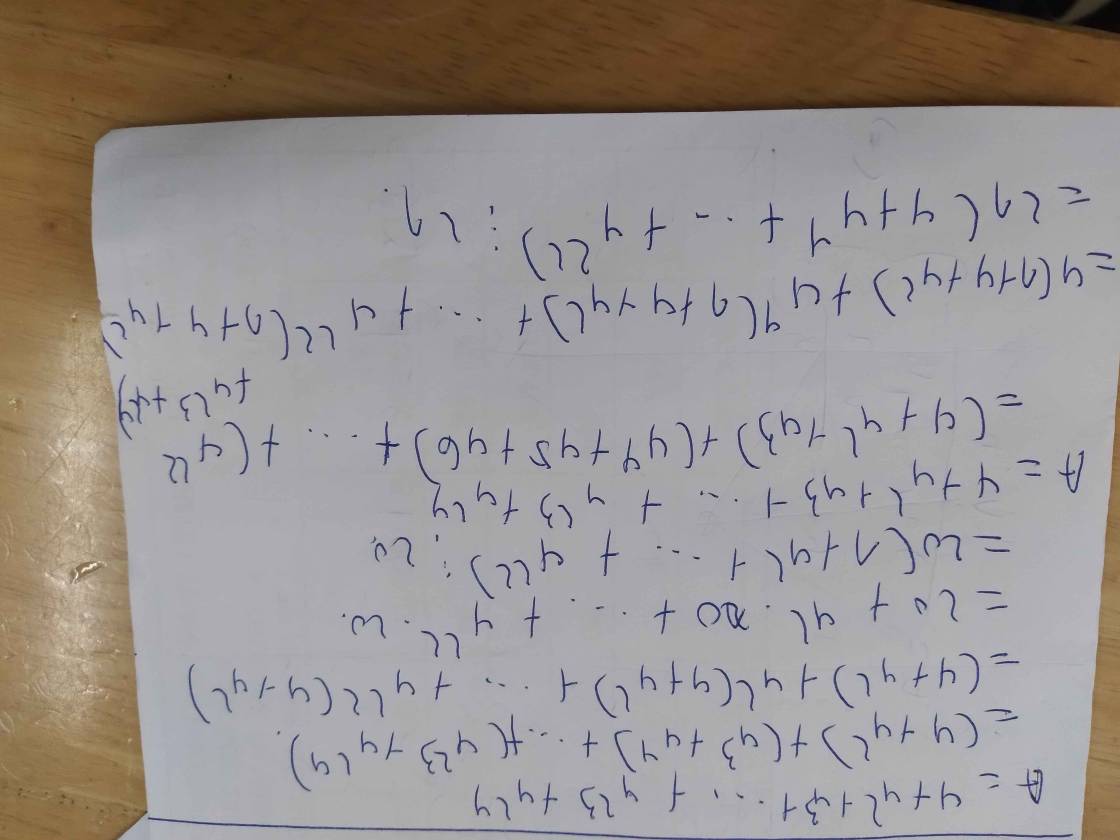
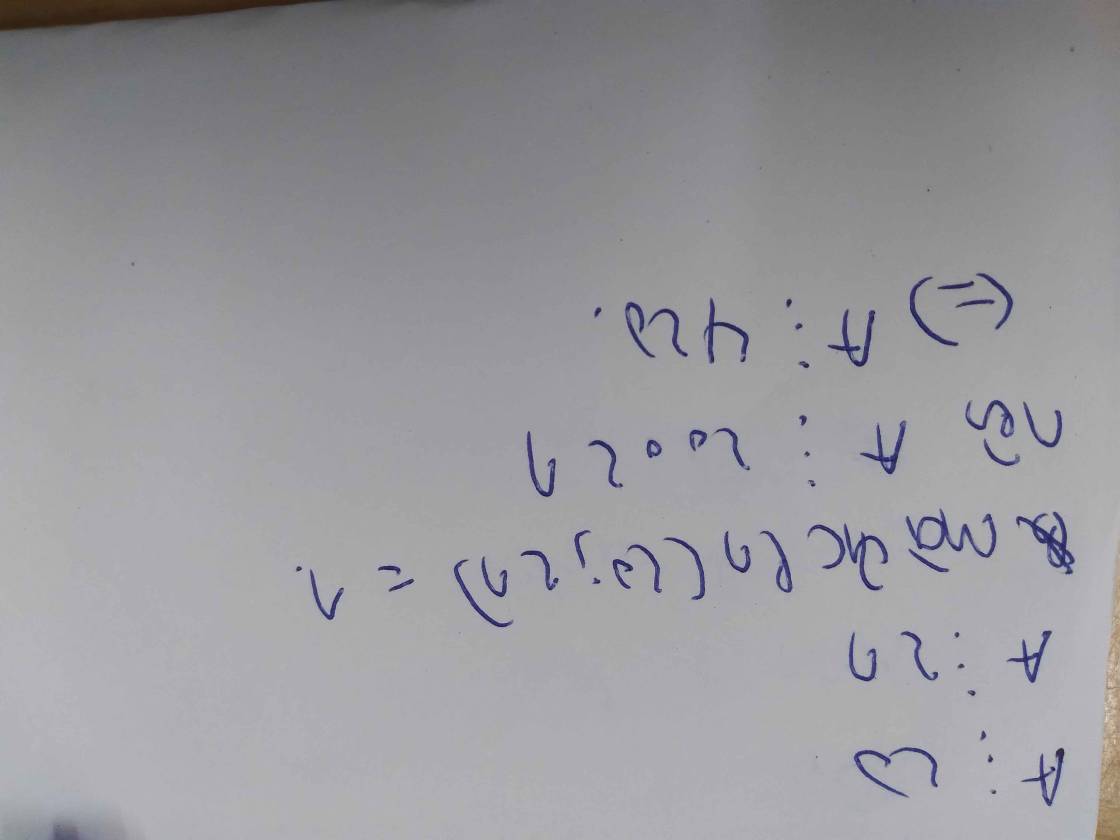
A=4+\(4^2\)+\(4^3\)+...+\(4^{23}\)+\(4^{24}\)
4A=\(4^2\)+\(4^3\)+\(4^4\)+...+\(4^{24}\)+\(4^{25}\)
4A-A=(\(4^2\)+\(4^3\)+\(4^4\)+...+\(4^{24}\)+\(4^{25}\))-(4+\(4^2\)+\(4^3\)+...+\(4^{23}\)+\(4^{24}\))
3A=\(4^{25}\)-4
A=(\(4^{25}\)-4):3
vậy A=(\(4^{25}\)-4):3
làm xong rùi đó
ít 1 lời cảm ơn
nhiều 1 cái tick xanh
nha!
\(4^2\)\(4^{25}\)
a = 4 + 42 + 43 + ... + 424
=> 2a = 42 + 43 + 44 + .... + 425
=> a = ( 42 + 43 + 44 + .... + 425 ) - ( 4 + 42 + 43 + ... + 424 )
=> a = 425 - 4
Vậy a = 425 - 4
chúc bạn học tốt