Cho tam giác ABC. Các đường phân giác của các góc ngoài tại B và C cắt nhau tại I. Chứng minh rằng AI là tia phân giác của góc A.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2023
Kẻ IK,IH,IE lần lượt vuông góc BC,AB,AC
Xét ΔBHI vuông tại H và ΔBKI vuông tại K có
BI chung
góc HBI=góc KBI
=>ΔBHI=ΔBKI
=>IH=IK
Xét ΔCKI vuông tại K và ΔCEI vuông tại E có
CI chung
góc KCI=góc ECI
=>ΔCKI=ΔCEI
=>IK=IE
=>IH=IE
Xét ΔAHI vuông tại H và ΔAEI vuông tại E có
AI chung
IH=IE
=>ΔAHI=ΔAEI
=>góc HAI=góc EAI
=>AI là phân giác của góc BAC
5 tháng 1 2018
1.Vì các tia phân giác của các góc B và C cắt nhau tại I
\(\Rightarrow\)I là giao của các đường phân giác trong tam giác
\(\Rightarrow\)AI là tia phân giác của góc A
A
20 tháng 6 2019
1.
Kẻ: \(ID\perp AB;IE\perp BC;IF\perp AC\)
\(\widehat{IDB}=\widehat{IEB}=90^0\)
\(\widehat{DBI}=\widehat{EIB}\left(gt\right)\)
BI cạnh huyền chung
⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\widehat{IEC}=\widehat{IFC}=90^0\)
\(\widehat{ECI}=\widehat{FCI}\left(gt\right)\)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
\(\widehat{IDA}=\widehat{IFA}=90^0\)
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra\(\widehat{DAI}=\widehat{FAI}\) (hai góc tương ứng)
Vậy AI là tia phân giác của \(\widehat{A}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
12 tháng 5 2022
a/ Xét tg BIC có
\(\widehat{BIC}=180^o-\left(\widehat{IBC}+\widehat{ICB}\right)=180^o-\dfrac{\widehat{B}}{2}-\dfrac{\widehat{C}}{2}=\)
\(=180^o-\left(\dfrac{\widehat{B}+\widehat{C}}{2}\right)=180^o-\left[\dfrac{180^o-\widehat{A}}{2}\right]=90^o+\dfrac{\widehat{A}}{2}\left(dpcm\right)\)
b/ Để c/m câu này ta chứng minh bài toán phụ: " Hai đường phân giác ngoài của 2 góc với đường phân giác trong của góc còn lại đồng quy"
Có hai đường phân giác của các góc ngoài của góc B và góc C cắt nhau tại J.
Từ J dựng các đường vuông góc với AB; AC; BC cắt 3 cạnh trên lần lượt tại D; E; F
Vì J thuộc đường phân giác của \(\widehat{DBC}\) nên JD=JF
Vì J thuộc đường phân giác của \(\widehat{ECB}\) nên JE=JF
(Mọi điểm thuộc đường phân giác của một góc thì cách đều hai cạnh của góc)
=> JD=JE
Xét tg vuông ADJ và tg vuông AEJ có
ẠJ chung; JD=JE (cmt) => tg ADJ = tg AEJ (hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{DAJ}=\widehat{EAJ}\) => Ạ là phân giác của góc \(\widehat{BAC}\)
Áp dụng vào bài toán:
Nối AJ => AJ là phân giác của \(\widehat{BAC}\) => AJ phải đi qua I (Trong tg 3 đường phân giác trong đồng quy) => A; I; J thẳng hàng
c/ Vì J; H; K bình đẳng nên B; I; K thẳng hàng và C; I; H thẳng hàng
=> AJ; BK; CH đồng quy tại I
CM
31 tháng 5 2018
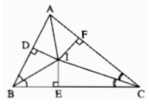
Kẻ: ID⊥AB, IE⊥BC, IF⊥AC
Xét hai tam giác vuông ΔIBD và ΔIEB, ta có:
∠(DBI) =∠(EBI) (gt)
∠(IDB) =∠(IEB) =90o
BI cạnh chung
Suy ra: ΔIDB= ΔIEB(cạnh huyền, góc nhọn)
Suy ra: ID = IE ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIEC và ΔIFC, ta có:
∠(ECI) =∠(FCI)
∠(IEC) =∠(IFC) =90o
CI cạnh huyền chung
Suy ra: ΔIEC= ΔIFC(cạnh huyền góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông ΔIDA và ΔIFA, ta có:
ID=IF
∠(IDA) =∠(IFA) =90o
AI cạnh huyền chung
Suy ra: ΔIDA= ΔIFA(cạnh huyền.cạnh góc vuông)
Suy ra: ∠(DAI) =∠(FAI) (hai góc tương ứng)
Vậy AI là tia phân giác góc A
CM
4 tháng 9 2019
Kẻ IH ⊥ AB, IJ ⊥ BC, IG ⊥ AC, KD ⊥ AB, KE ⊥ AC, KF ⊥ BC
Vì I nằm trên tia phân giác của ∠(BAC) nên IH = IG (tính chất tia phân giác)
Vì I nằm trên tia phân giác của ∠(BCA) nên IJ = IG (tính chất tia phân giác)
Suy ra: IH = IJ
Do đó I nằm trên tia phân giác của ∠(ABC) (1)
Vì K nằm trên tia phân giác của ∠(DAC) nên KD = KE (tính chất tia phân giác)
Vì K nằm trên tia phân giác của ∠(ACF) nên KE = KF (tính chất tia phân giác)
Suy ra: KD = KF
Do đó K nằm trên tia phân giác của ∠(ABC) (2)
Từ (1) và (2) suy ra: B, I, K thẳng hàng.
AH
Akai Haruma
Giáo viên
6 tháng 5 2021
Lời giải:
Kẻ $KM, KT, KN$ lần lượt vuông góc với $AB, AC, BC$.
Vì $K$ thuộc tia phân giác $\widehat{MAC}$ nên $KM=KT$ (tính chất quen thuộc)
Vì $K$ thuộc tia phân giác $\widheat{ACN}$ nên $KN=KT$
$\Rightarrow KM=KN$
$\Rightarrow K$ thuộc tia phân giác $\widehat{MBN}$ hay $\widehat{ABC}$
Do đó $BI, BK$ cùng là tia phân giác $\widehat{ABC}$
$\Rightarrow B,I,K$ thẳng hàng
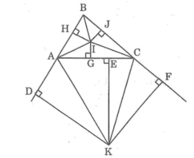
vẽ hình nữa nha