cho tam giác abc vuông tại a . trên cạnh bc lấy điểm e sao cho be=ba. tia phân giác góc B cắt AC ở D . : a ) so sánh DA và DE ; b ) tính số đo góc BED
lm gấp giúp mik nhé
hi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Xét tam giác ABD và tam giác EBD, có :
AB=EB ( gt)
góc B1= góc B2(BD là p/giác góc ABE) }=>tam giác ABD = tam giác EBD
BD chung
=> AD=DE (2 cạnh tg ứng)
b) Vì tam giác ABD = tam giác EBD (c/m a)
=> góc BAD=góc BED
Mà góc BAD=90 độ
=>góc BED=90 độ
Vây góc BED=90 độ
a) Xét tam giác ABD và EBD có: AB = BE ; góc ABD = EBD; BD chung
=> tam giác ABD = EBD (c - g - c)
=> AD = DE và BAD = BED = 90o

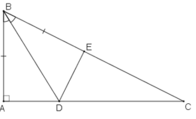
Xét ΔABD và ΔEBD, ta có:
AB = BE (gt)
∠(ABD) = ∠(DBE) (vì BD là tia phân giác)
BC cạnh chung
Suy ra: ΔABD = ΔEBD(c.g.c)
⇒ DA = DE (hai cạnh tương ứng)

a) xét ΔABD và ΔEBD có:
BA = BE (GT)
∠ABD=∠EBD( BD là tia phân giác ∠ABE)
BD chung⇒ΔABD=ΔEBD(ch-cgv)
⇒AD=ED (2 cạnh tương ứng)
b)Vì ΔABD=ΔEBD(CMT)
⇒∠BAD=∠BED(2 góc tương ứng)
Mà ∠BAD= 90 độ
⇒∠BED = 90 độ

a)Xét tam giác ABD và tam giác EBD, có :
AB=EB ( gt)
góc B1= góc B2(BD là p/giác góc ABE) }=>tam giác ABD = tam giác EBD
BD chung
=> AD=DE (2 cạnh tg ứng)
b) Vì tam giác ABD = tam giác EBD (c/m a)
=> góc BAD=góc BED
Mà góc BAD=90 độ
=>góc BED=90 độ
Vây góc BED=90 độ

a/ Xét tg ABD và tg EBD có:
BD chung
AB = BE (gt)
góc ABD = góc EBD ( BD là pg góc B)
=> tg ABD = tg EBD (c-g-c)
=> \(\left\{{}\begin{matrix}\text{AD = DE (2 cặp cạnh tương ứng)}\\\text{góc BAD = góc BED (2 cặp góc tương ứng)}\end{matrix}\right.\)
mà góc BAD = 90 ( tg ABC vuông tại A)
=> góc BED = 90
=> DE vuông góc BC
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
b: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)