y=x3-2x2+4x-5
viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến có hệ số góc nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C
- Ta có:
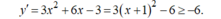
- Hệ số góc của tiếp tuyến đồ thị hàm số y = x 3 + 3 x 2 – 3 x là một giá trị của y’, nên hệ số góc nhỏ nhất là k = -6, ứng với hoành độ tiếp điểm là x = -1 ⇒ y = 5.
→ Phương trình tiếp tuyến là:
y = -6(x + 1) + 5, hay y = -6x - 1.

Đáp án D
Gọi M a ; b là điểm thuộc đồ thị hàm số có tiếp tuyến thỏa mãn đề bài.
Ta có y ' = 3 x 2 − 6 x + 6 ⇒ y ' a = 3 a 2 − 6 a + 6 = 3 a − 1 2 + 3 ≥ 3 ⇒ min y ' a = 3 ⇔ a = 1
Suy ra y 1 = 9 ⇒ P T T T tại M 1 ; 9 là y = 3 x − 1 + 9 y = 3 x + 6

Đáp án B
Có
y ' = x 2 − 2 x + 2 y ' ' = 6 x − 2
Tiếp tuyến có hệ số góc nhỏ nhất là nghiệm của y ' ' = 0 ⇔ x = 1 3
⇒ y ' 1 3 = 5 3
Ta có: \(y'=3x^2-4x+4=3\left(x^2-\dfrac{4}{3}x+\dfrac{4}{9}\right)+\dfrac{8}{3}=3\left(x-\dfrac{2}{3}\right)^2+\dfrac{8}{3}\ge\dfrac{8}{3}\forall x\in R\)
⇒ y'min = 8/3 tại x0 = 2/3
⇒ y0 = -79/27
⇒ PTTT: \(y=\dfrac{8}{3}\left(x-\dfrac{2}{3}\right)-\dfrac{79}{27}\)