Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
- Ta có:
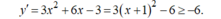
- Hệ số góc của tiếp tuyến đồ thị hàm số y = x 3 + 3 x 2 – 3 x là một giá trị của y’, nên hệ số góc nhỏ nhất là k = -6, ứng với hoành độ tiếp điểm là x = -1 ⇒ y = 5.
→ Phương trình tiếp tuyến là:
y = -6(x + 1) + 5, hay y = -6x - 1.

Chọn A.
Đạo hàm: y’ = 3x2 – 6x = 3(x – 1)2 – 3 ≥ -3 với mọi x.
Vậy trong các tiếp tuyến tại các điểm trên đồ thị hàm số đã cho, tiếp tuyến có hệ số góc nhỏ nhất bằng -3.

Chọn C.
Ta có y’ = f’(x) = 3x2 + 6x – 9
Gọi xo là hoành độ tiếp điểm của tiếp tuyến, vậy f’(xo) = 3x02 + 6xo – 9
Ta có 3x02 + 6xo – 9 = 3(xo2 + 2xo + 1) – 12 = 3(xo + 1)2 – 12 ≥ -12, ∀xo ∈ (C)
Vậy mìn’(x0) = -12 tại xo = -1 ⇒ yo = 16
Suy ra phương trình tiếp tuyến cần tìm: y = -12(x + 1) + 16 hay y = -12x + 4.

Hệ số góc của tiếp tuyến: y ' = 4 x 3 + 3 x 2 − 4 x ⇒ y ' − 1 = 3 .
Chọn đáp án C

Đặt \(y=f(x)=x^3+2x^2+x-1 \)
\(f'(x)=3x^2+4x+1\)
Phương trình tiếp tuyến của đồ thị hàm số y tại M là:
\(y=f'(x_m)(x-x_m)+f(x_m)=f'(1)(x-1)+f(1)=8(x-1)+3=8x-5 \)

" Tìm k để có 2 tiếp tuyến của đồ thị có cùng hệ số góc k"
Đọc câu này mà não load không nổi luôn :D
Đọc đi đọc lại không hiểu đề bài muốn nói đến điều gì

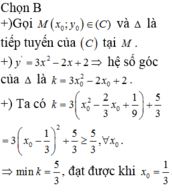
Ta có: \(y'=3x^2-4x+4=3\left(x^2-\dfrac{4}{3}x+\dfrac{4}{9}\right)+\dfrac{8}{3}=3\left(x-\dfrac{2}{3}\right)^2+\dfrac{8}{3}\ge\dfrac{8}{3}\forall x\in R\)
⇒ y'min = 8/3 tại x0 = 2/3
⇒ y0 = -79/27
⇒ PTTT: \(y=\dfrac{8}{3}\left(x-\dfrac{2}{3}\right)-\dfrac{79}{27}\)