Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo định lí Pytago tam giác DEF vuông tại D
\(DF=\sqrt{EF^2-DE^2}=16cm\)
b, Xét tam giác EDF và tam giác DHF
^DFE _ chung
^EDF = ^DHF = 900
Vậy tam giác EDF ~ tam giác DHF (g.g)
\(\dfrac{EF}{DF}=\dfrac{DF}{HF}\Rightarrow DF^2=EF.HF\)
a: \(DF=\sqrt{20^2-12^2}=16\left(cm\right)\)
b: Xét ΔEDF vuông tại D và ΔDHF vuông tại H có
góc F chung
Do đó: ΔEDF\(\sim\)ΔDHF
a, Theo định lí Pytago tam giác DEF vuông tại D
\(DF=\sqrt{EF^2-DE^2}=16cm\)
b, Xét tam giác EDF và tam giác DHF có
^EFD _ chung, ^EDF = ^DHF = 900
Vậy tam giác EDF ~ tam giác DHF (g.g)
\(\dfrac{EF}{DF}=\dfrac{DF}{HF}\Rightarrow DF^2=EF.HF\)
a: \(EF=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xet ΔEDF có EK là phân giác
nên DK/DE=FK/FE
=>DK/3=FK/5=(DK+FK)/(3+5)=8/8=1
=>DK=3cm; FK=5cm
b: Xet ΔDEK vuông tại D và ΔHEI vuông tại H có
góc DEK=góc HEI
=>ΔDEK đồng dạng với ΔHEI
=>ED/EH=EK/EI
=>ED*EI=EK*EH
c: góc DKI=90 độ-góc KED
góc DIK=góc HIE=90 độ-góc KEF
mà góc KED=góc KEF
nên góc DKI=góc DIK
=>ΔDKI cân tại D
mà DG là trung tuyến
nên DG vuông góc IK
hình tự kẻ
tứ giác ADBH có:
D vuông (gt)
Góc HAD vuông ( AH vuông DE )
Góc HBD vuông ( BH vuông DF )
=> tứ giác ADBH là HCN
=> AB=DH; I là trung điểm của AB và DH ( tính chất hcn )
Ta có:
AB=DH (cmt)
I là trung điểm của AB và DH (cmt)
=> IH = IB
Tam giác HIB có:
IH = IB (cmt)
=> tam giác HIB cân tại I
=> góc IHB = góc IBH (2 góc đáy trong tam giác cân )
a: Xét ΔEHD vuông tại H và ΔEDF vuông tại D có
góc E chung
=>ΔEHD đồng dạng với ΔEDF
Xét ΔFHD vuông tại H và ΔFDE vuông tại D có
góc F chung
=>ΔFHD đồng dạng với ΔFDE
Xét ΔHDE vuông tại H và ΔHFD vuông tại H có
góc HDE=góc HFD
=>ΔHDE đồng dạng với ΔHFD
b: EF=căn 6^2+8^2=10cm
DH=6*8/10=4,8cm
HE=6^2/10=3,6cm
HF=10-3,6=6,4cm
a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có
DE=DF
DH chung
Do đó:ΔDHE=ΔDHF
b: EF=8cm nên HE=4cm
=>DH=3cm
c: Xét ΔDMH vuông tại M và ΔDNH vuông tại N có
DH chung
\(\widehat{MDH}=\widehat{NDH}\)
Do đó:ΔDMH=ΔDNH
Suy ra: HM=HN
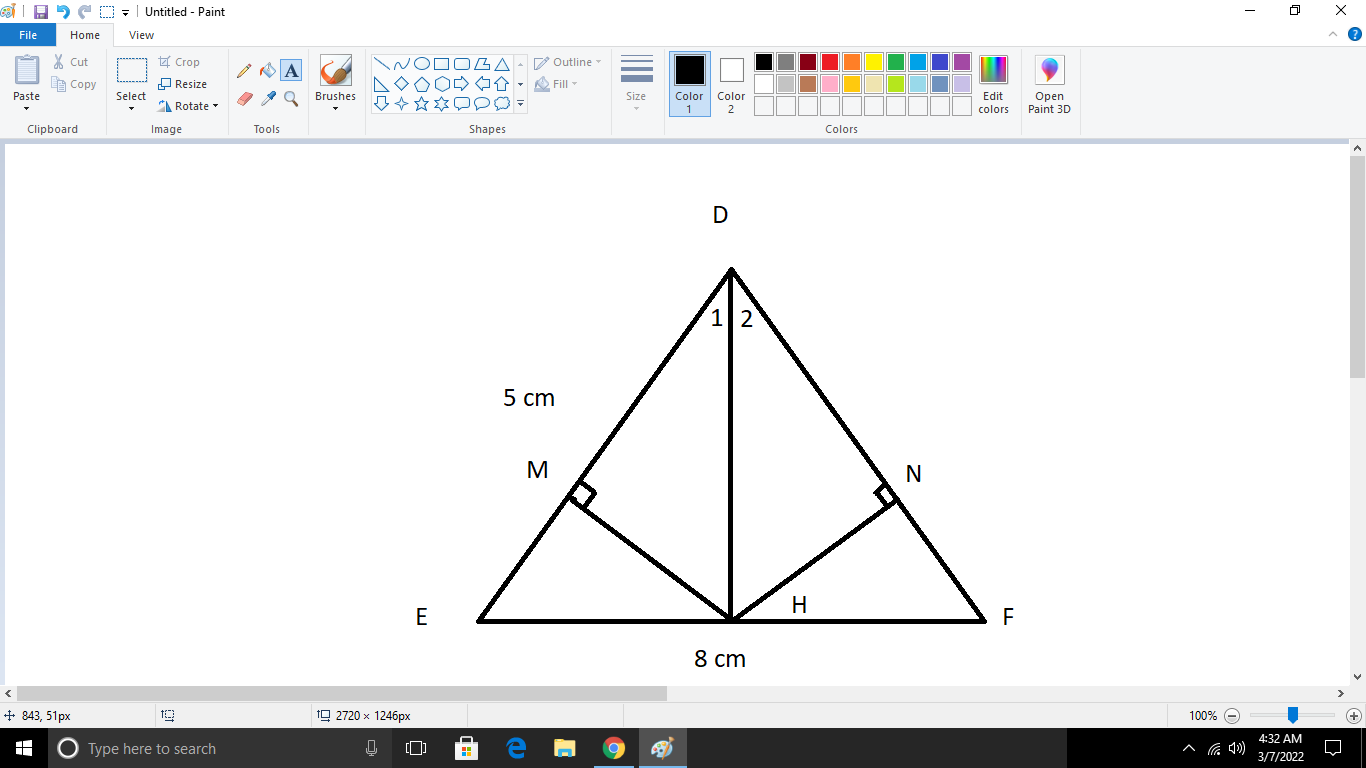
\(\text{a)}\text{Vì }\Delta DEF\text{ cân tại D}\)
\(\Rightarrow DE=DF\)
\(\widehat{E}=\widehat{F}\)
\(\text{Xét }\Delta DHE\text{ và }\Delta AHF\text{ có:}\)
\(DE=DF\left(cmt\right)\)
\(BH\text{ chung}\)
\(\widehat{E}=\widehat{F}\left(cmt\right)\)
\(\Rightarrow\Delta DHE=\Delta DHF\left(c-g-c\right)\)
\(\Rightarrow EH=HF\text{(hai cạnh tương ứng)}\)
\(\text{b)}\text{Vì }EH=HF\left(cmt\right)\)
\(\Rightarrow EH=\dfrac{EF}{2}=\dfrac{8}{2}=4\left(cm\right)\)
\(\text{Xét }\Delta DEH\text{ có:}\)
\(DE^2=DH^2+EH^2\)
\(\Rightarrow DH^2=DE^2-EH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow DH^2=5^2-4^2=25-16=9\left(cm\right)\)
\(\Rightarrow DH=\sqrt{9cm}=3\left(cm\right)\)
\(\text{c)Xét }\Delta HMD\text{ và }\Delta HND\text{ có:}\)
\(DH\text{ chung}\)
\(\widehat{D_1}=\widehat{D_2}\left(\Delta DHE=\Delta DHF\right)\)
\(\widehat{DMH}=\widehat{DNH}=90^0\)
\(\Rightarrow\Delta HMD=\Delta HND\left(ch-cgv\right)\)
\(\Rightarrow HM=HN\text{( hai cạnh tương ứng)}\)
a: ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
=>\(EF^2=32^2+24^2=1600\)
=>EF=40(cm)
Xét ΔDEF vuông tại D có DH là đường cao
nên \(DH\cdot FE=DE\cdot DF\)
=>\(DH\cdot40=32\cdot24=768\)
=>DH=768/40=19,2(cm)
Xét ΔDFE vuông tại D có DH là đường cao
nên \(EH\cdot EF=DE^2\)
=>\(EH\cdot40=32^2\)
=>\(EH=\dfrac{1024}{40}=25,6\left(cm\right)\)
b: Xét ΔDHE vuông tại H có HA là đường cao
nên \(DA\cdot DE=DH^2\left(1\right)\)
Xét ΔDHF vuông tại H có HB là đường cao
nên \(DB\cdot DF=DH^2\left(2\right)\)
Từ (1) và (2) suy ra \(DA\cdot DE=DB\cdot DF\)
=>\(\dfrac{DA}{DF}=\dfrac{DB}{DE}\)
Xét ΔDAB vuông tại A và ΔDFE vuông tại D có
\(\dfrac{DA}{DF}=\dfrac{DB}{DE}\)
Do đó: ΔDAB đồng dạng với ΔDFE
c: Xét tứ giác DAHB có
\(\widehat{DAH}=\widehat{DBH}=\widehat{ADB}=90^0\)
=>DAHB là hình chữ nhật
=>DH=AB
\(DH^2\cdot sin^2E+DH^2\cdot sin^2F\)
\(=AB^2\cdot sin^2E+AB^2\cdot sin^2F\)
\(=AB^2\left(sin^2E+sin^2F\right)=AB^2\cdot\left(sin^2E+cos^2E\right)=AB^2\)