Tìm TXĐ và vẽ BBT của hàm số: y = x3 - 2x2 + x - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Điều kiện đồng biến, nghịch biến của hàm số:
Cho hàm số y = f(x) có đạo hàm trên khoảng K.
+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.
+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.
- Xét hàm số
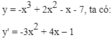
+ Hàm số đồng biến
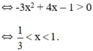
+ Hàm số nghịch biến
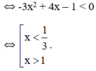
Vậy hàm số đồng biến trên 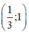
nghịch biến trên các khoảng 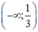 và (1; +∞)
và (1; +∞)
- Xét hàm số 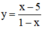
Ta có: D = R \ {1}
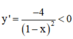 ∀ x ∈ D.
∀ x ∈ D.
⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).

Đáp án C.
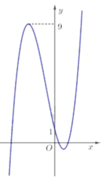
Ta có đồ thị hàm số y = x 3 + 2 x 2 − 4 x + 1 như hình vẽ bên. Dễ thấy đường thẳng y = 2 cắt đồ thị hàm số y = x 3 + 2 x 2 − 4 x + 1 tại 3 điểm phân biệt

Đáp án D
Ta có y ' = 3 x 2 − 4 x + 1 ⇒ y ' = 0 ⇔ x = 1 x = 1 3
Suy ra y − 1 = − 3 , y 1 3 = 31 27 , y 1 = 1 ⇒ max − 1 ; 1 y = 31 27

ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)

Ta có y ' = 3 x 2 - 4 x + m
Hàm số đạt cực trị tại x = 1 thì y'(1) = 0 ⇒ 3 . 1 2 - 4 . 1 + m = 0 ⇒ m = 1
Với m = 1 thì hàm số đã cho trở thành y = x 3 - 2 x 2 + x + 1
Ta có y ' = 3 x 2 - 4 x + 1 , y'' = 6x - 4 Vì y''(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1.
Do vậy không có m thỏa mãn. Chọn đáp án D.
Chú ý. Sai lầm có thể gặp phải: khi giải y'(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.

Đáp án A.
Ta có: y’ = -3x2 + 4x + m.
y’’ = -6x + 4.
+ y’(1) = 0 <=> -3 + 4 + m = 0 ó m = -1.
+ y’’(1) = -2 < 0 thỏa
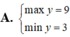
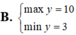
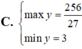
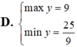
TXĐ: \(D=R\)
\(y=x^3-2x^2+x-1\\ \Rightarrow y'=3x^2-4x+1\)
\(y'=0\Leftrightarrow3x^2-4x+1=0 \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)
Bảng biến thiên: