K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

H
6 tháng 6 2023
Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.

CM
23 tháng 3 2017
Chọn B.
Đạo hàm: y’ = 3x2 – 2mx + 2m – 3 và y” = 6x – 2m
+ Để hàm số đạt cực đại x = 1 thì:
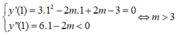
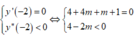
 (không tồn tại m).
(không tồn tại m).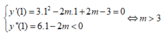

Ta có y ' = 3 x 2 - 4 x + m
Hàm số đạt cực trị tại x = 1 thì y'(1) = 0 ⇒ 3 . 1 2 - 4 . 1 + m = 0 ⇒ m = 1
Với m = 1 thì hàm số đã cho trở thành y = x 3 - 2 x 2 + x + 1
Ta có y ' = 3 x 2 - 4 x + 1 , y'' = 6x - 4 Vì y''(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1.
Do vậy không có m thỏa mãn. Chọn đáp án D.
Chú ý. Sai lầm có thể gặp phải: khi giải y'(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.