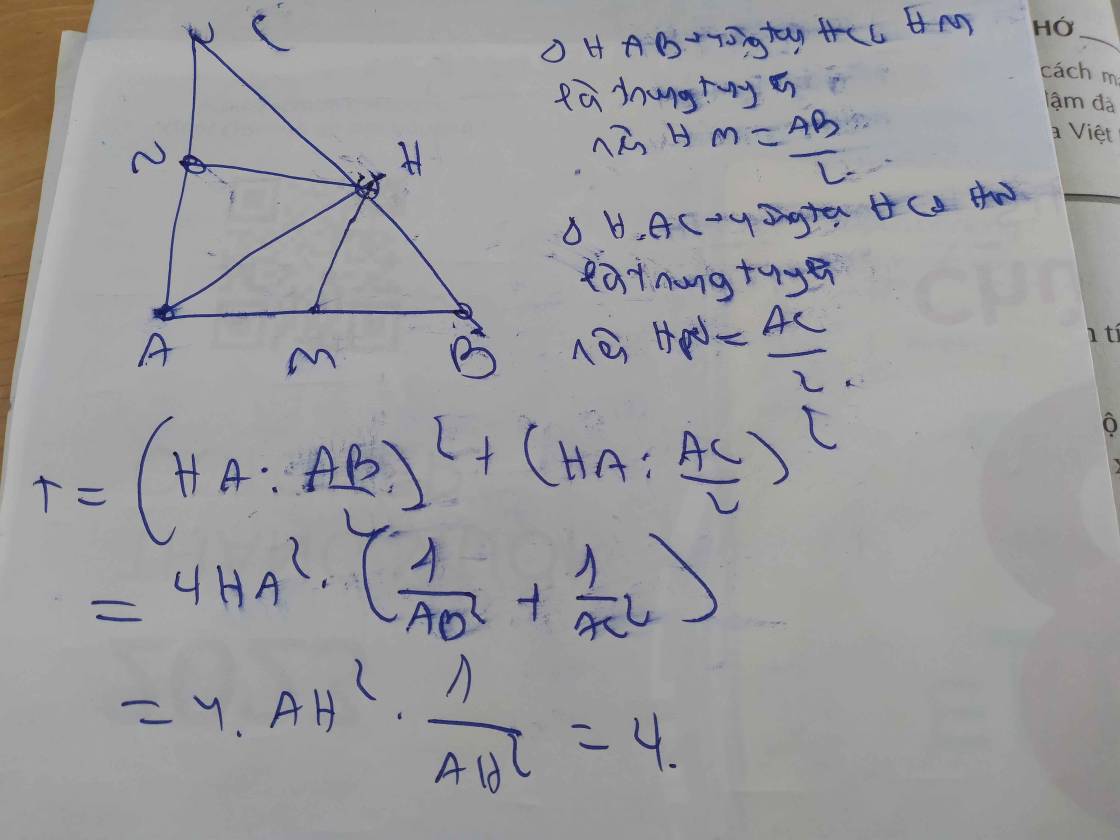
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC.
Tính giá trị của biểu thức: T = (HA/HM)2 + (HA/HN)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
11 tháng 10 2023
Đúng(1)
Những câu hỏi liên quan
18 tháng 6 2023
HN//AB
=>góc NHA=góc HAM
=>góc NHA=góc MHA
=>HA là phân giác của góc NHM
HC vuông góc HA
=>HC là phân giác ngoài của ΔIHN
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
25 tháng 3 2016
a/ Ta có AN vuông góc AC; HM vuông góc AC => AN//HM (1)
Ta có AM vuông góc AB; HN vuông góc AB => AM//HN (2)
=> Tứ giác AMHN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
AH; MN là hai đường chéo của hbh nên chúng cắt nhau tại trung điểm mỗi đường
b/ Trước hết ta phải c/m A, I, K thẳng hàng
Nối AI; AK
+ Xét tam giác AHK có
Hình bình hành AMHN có ^MAN=90 => ^ANM =90 => AN vuông góc HK nà NK=NH
=> tam giác AKH cân tại A (Tam giác có đường cao đồng thời là đường trung tuyến là tam giác cân)
=> ^KAN=^HAN (1) (trong tam giác cân đường cao đồng thời là đường phân giác)
+ Xét tam giác AIH chứng minh tương tự ta cũng có
^HAM=^IAM (2)
+ Mà ^HAN+^HAM=^BAC=90 (3)
Từ (1) (2) (3) => ^KAN+^IAM=^HAN+^HAM=90
=> ^KAN+^HAN+HAM+^IAM=180 => A,I,K thẳng hàng
+ Ở trên ta đã chứng minh được tam giác AKH và tam giác AIH là tam giác cân tại A
=> AK=AH=AI => A là trung điểm của IK
+ Xét tam giác
13 tháng 5 2019
a)Do A thuộc đường trung trực của HM nên AH=AM
Do a thuộc đường trung trực của HN nên AH=AN
Suy ra:AM=AN
Suy ra:tam giác AMN cân
