Vẽ hình thoi MNPQ biết góc MNP bằng \(60^\circ \) và MN=6 cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


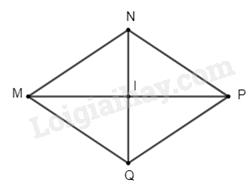
a) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(IM = IP\) và \(NQ \bot MP\)
Suy ra \(\widehat {{\rm{MIN}}} = 90\)
Xét tam giác vuông \(MPI\) (vuông tại \(I\)) ta có:
\(M{I^2} = M{N^2} - N{I^2} = {10^2} - {6^2} = 100 - 36 = 64\) (định lý Pythagore)
Suy ra \(MI = 8\) (dm)
b) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(NI\) là phân giác của \(\widehat {MNP}\)
Suy ra \(\widehat {MNI} = \widehat {PNI} = \frac{{128^\circ }}{2} = 64^\circ \)
Xét \(\Delta MNI\) vuông tại \(I\) ta có:
\(\widehat {{\rm{MNI}}} + \widehat {{\rm{NMI}}} = 90\)
Suy ra \(\widehat {IMN} = 90^\circ - \widehat {MNI} = 90^\circ - 64^\circ = 26^\circ \)

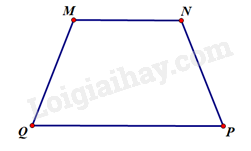
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)

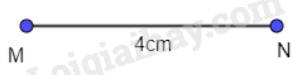
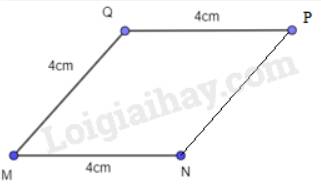
Cách 1: - Vẽ đoạn thẳng MN = 4 cm.
- Lấy M tâm, vẽ đường tròn bán kính 4 cm (hình vẽ).
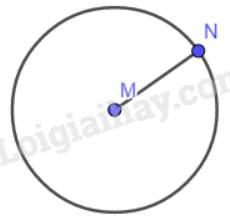
- Trên đường tròn lấy điểm Q, nối M với Q. Khi đó MQ= 4cm.

- Qua N và Q lần lượt vẽ hai đường tròn bán kính bằng 4 cm, hai đường tròn này cắt nhau tại M và P (P khác M).

- Nối P với N và P với Q ta được hình thoi MNPQ. Các cạnh PN=QP =4cm.
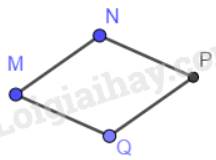
Nhận xét: Hình vẽ có tính chất các cạnh MN=NP=PQ=QM =4cm
Góc \(\widehat {MNQ}\) khác nhau thì sẽ tạo được các hình thoi khác nhau.
Cách 2:
- Vẽ đoạn thẳng MN = 4 cm
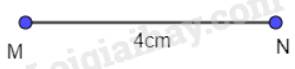
- Vẽ đoạn thẳng MQ = 4 cm
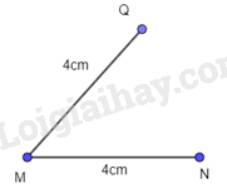
- Từ Q vẽ đường thẳng song song với MN, trên đường thẳng đó lấy điểm P sao cho PQ = 4 cm.
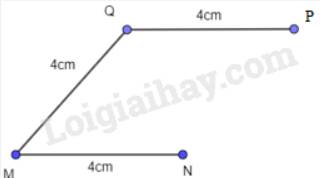
- Nối P với N ta được hình thoi MNPQ.

a) Diện tích hình thoi MPNQ là:
\(S_{MPNQ}=\frac{1}{2}. MN. PQ=\frac{1}{2}. 8.6=24 (cm^2)\)
b) Chu vi hình thoi MPNQ là:
\(C_{MPNQ}=4. MP = 4. 5 = 20 (cm)\)

a: Xét tứ giác ABQM có
AM//QB
AM=QB
DO đó: ABQM là hình bình hành
mà MA=MQ
nên ABQM là hình thoi
b: Xét tứ giác ANBQ có
AN//BQ
AN=BQ
Do đó: ANBQ là hình bình hành
Suy ra: AQ//BN
c: Xét tứ giác ANPB có
AN//BP
AN=BP
Do đó: ANPB là hình bình hành
mà NA=NP
nên ANPB là hình thoi
Xét ΔQPA có
AB là đường trung tuyến
AB=QP/2
Do đó:ΔQPA vuông tại A
hay \(\widehat{QAP}=90^0\)
- Kẻ đoạn MN = 6cm, đo góc MNP bằng \(60^\circ \). Lấy điểm P trên tia còn lại của góc (không chứa điểm M) sao cho NP = 6cm.
Cách 1: - Nối M với P. Lấy O là trung điểm của MP.
- Kẻ đường thẳng NO, lấy điểm Q sao cho OQ=ON( Q khác N).
- Nối MQ, QP ta được hình thoi như hình vẽ:
Cách 2:
- Qua M kẻ đường thẳng song song NP, trên đó lấy điểm Q sao cho MQ = 6cm
- Nối PQ
Ta được hình thoi MNPQ cần vẽ