QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 10 2023
Tham khảo:
Cách 1:
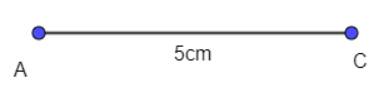
Vẽ đoạn thẳng AC = 5 cm.
Lấy trung điểm O của AC.
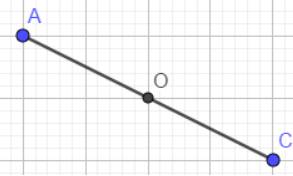
Qua O kẻ đoạn thẳng BD =7cm (B và D khác phía nhau so với AC) sao cho O là trung điểm của BD (tức là OB=OD=3,5cm).
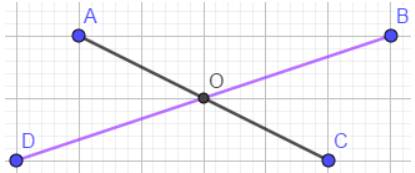
Nối A với B, A với D, B với C, C với D ta được hình bình hành ABCD.
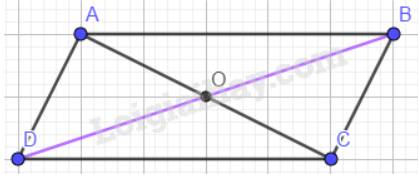
Sử dụng thước đo các cạnh ta thấy AB=CD, AD=BC.
Hình vừa vẽ sử dụng tính chất hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.
Cách 2:
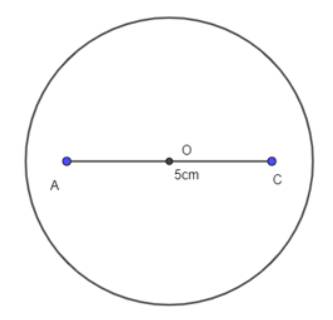
Vẽ đoạn thẳng AC = 5 cm.
Lấy trung điểm O của đoạn thẳng AC. Vẽ đường tròn tâm O bán kính 3,5 cm.
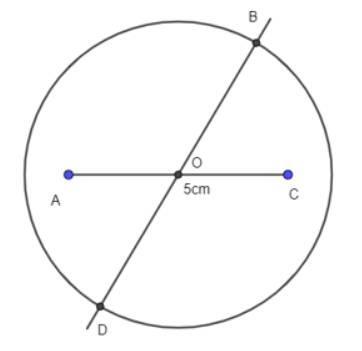
Vẽ đường thẳng đi qua tâm O cắt đường tròn tại hai điểm B và D.
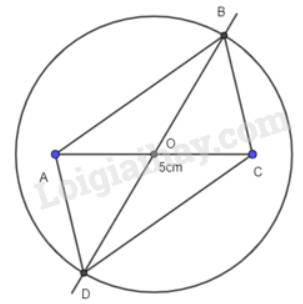
Nối A với B, B với C, C với D, D với A, ta được hình bình hành ABCD.
QT
1
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
- Kẻ đoạn MN = 6cm, đo góc MNP bằng \(60^\circ \). Lấy điểm P trên tia còn lại của góc (không chứa điểm M) sao cho NP = 6cm.
Cách 1: - Nối M với P. Lấy O là trung điểm của MP.
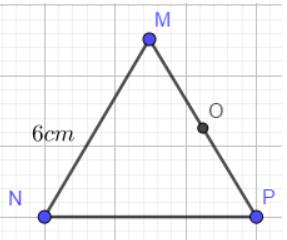
- Kẻ đường thẳng NO, lấy điểm Q sao cho OQ=ON( Q khác N).
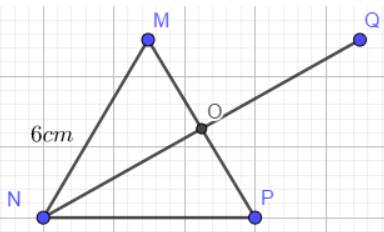
- Nối MQ, QP ta được hình thoi như hình vẽ:
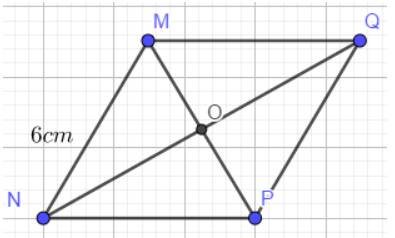
Cách 2:
- Qua M kẻ đường thẳng song song NP, trên đó lấy điểm Q sao cho MQ = 6cm
- Nối PQ
Ta được hình thoi MNPQ cần vẽ
QT
1
10 tháng 10 2023
Tham khảo:
a)
- Kẻ đoạn thẳng AB=5cm.
- Dùng compa vẽ 2 đường tròn bán kính 5cm có tâm lần lượt là A và B.
- Điểm C là giao điểm của hai đường tròn đó.
ABC là tam giác đều cần vẽ.
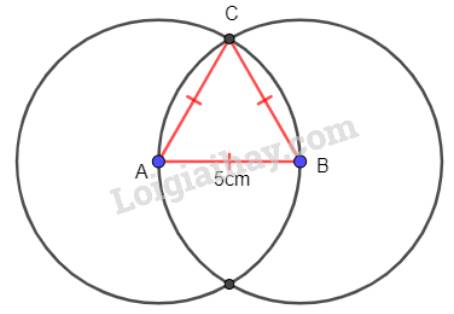
b)
- Vẽ đoạn thẳng AB=5cm và đoạn thẳng AD=3cm vuông góc với nhau.
- Qua B kẻ đường thẳng vuông góc với AB.
- Qua D kẻ đường thẳng vuông góc với AD.
- Hai đường thẳng này cắt nhau ở C.
ABCD là hình chữ nhật cần vẽ.
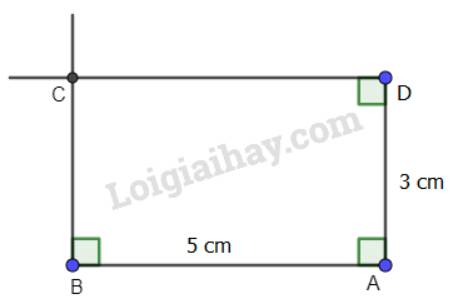
c)
- Vẽ đoạn thẳng CD dài 3cm.
- Vẽ hai đường thẳng vuông góc với CD tại C và D như hình vẽ.
- Trên đường thẳng qua C lấy đoạn thẳng CB=3cm; trên đường thẳng qua D lấy đoạn thẳng DA=3cm.
- Nối 2 điểm A và B ta được hình vuông cần vẽ.
d)
- Vẽ đoạn thẳng AB=6cm.
- Vẽ đường tròn tâm A bán kính 8cm.
- Qua A kẻ đường thẳng vuông góc với AB. Trên đường thẳng lấy H sao cho AH=4cm.
- Qua H kẻ đường thẳng vuông góc với AH cắt đường tròn tại điểm D (chọn 1 trong 2 giao điểm).
- Qua B kẻ đường thẳng song song với AD.
- Qua D kẻ đường thẳng song song với AB.
- Hai đường thẳng cắt nhau tại C.
ABCD là hình bình hành cần vẽ.
e)
- Vẽ đoạn thẳng AB = 5cm.
- Vẽ đường tròn tâm A bán kính 5 cm. Trên đường tròn này lấy điểm D.
- Từ D vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm C sao cho DC = 5 cm.
- Nối C với B ta được hình thoi ABCD có cạnh 5 cm.
Ta được ABCD là hình thoi cần vẽ.
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
a) Diện tích hình thoi MPNQ là:
\(S_{MPNQ}=\frac{1}{2}. MN. PQ=\frac{1}{2}. 8.6=24 (cm^2)\)
b) Chu vi hình thoi MPNQ là:
\(C_{MPNQ}=4. MP = 4. 5 = 20 (cm)\)
10 tháng 9 2023
Cạnh QN dài :
\(\left(26+6\right):2=18\left(cm\right)\)
Cạnh MN dài :
\(26-18=8\left(cm\right)\)
Tổng 4 cạnh hình thoi là :
\(8.4=32\left(cm\right)\)
Đáp số...
10 tháng 9 2023
Đính chính
\(QN=\left(26+6\right):2=16\left(cm\right)\)
\(MN=26-16=10\left(cm\right)\)
Bốn cạnh dài :
\(10.4=40\left(cm\right)\)
Cách 1: - Vẽ đoạn thẳng MN = 4 cm.
- Lấy M tâm, vẽ đường tròn bán kính 4 cm (hình vẽ).
- Trên đường tròn lấy điểm Q, nối M với Q. Khi đó MQ= 4cm.
- Qua N và Q lần lượt vẽ hai đường tròn bán kính bằng 4 cm, hai đường tròn này cắt nhau tại M và P (P khác M).
- Nối P với N và P với Q ta được hình thoi MNPQ. Các cạnh PN=QP =4cm.
Nhận xét: Hình vẽ có tính chất các cạnh MN=NP=PQ=QM =4cm
Góc \(\widehat {MNQ}\) khác nhau thì sẽ tạo được các hình thoi khác nhau.
Cách 2:
- Vẽ đoạn thẳng MN = 4 cm
- Vẽ đoạn thẳng MQ = 4 cm
- Từ Q vẽ đường thẳng song song với MN, trên đường thẳng đó lấy điểm P sao cho PQ = 4 cm.
- Nối P với N ta được hình thoi MNPQ.