Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

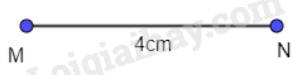
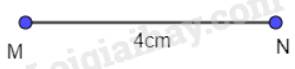
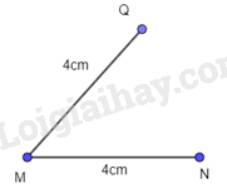
Cách 1: - Vẽ đoạn thẳng MN = 4 cm.
- Lấy M tâm, vẽ đường tròn bán kính 4 cm (hình vẽ).
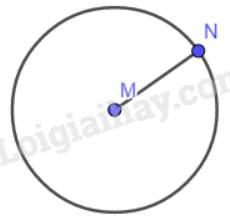
- Trên đường tròn lấy điểm Q, nối M với Q. Khi đó MQ= 4cm.

- Qua N và Q lần lượt vẽ hai đường tròn bán kính bằng 4 cm, hai đường tròn này cắt nhau tại M và P (P khác M).

- Nối P với N và P với Q ta được hình thoi MNPQ. Các cạnh PN=QP =4cm.
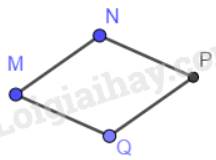
Nhận xét: Hình vẽ có tính chất các cạnh MN=NP=PQ=QM =4cm
Góc \(\widehat {MNQ}\) khác nhau thì sẽ tạo được các hình thoi khác nhau.
Cách 2:
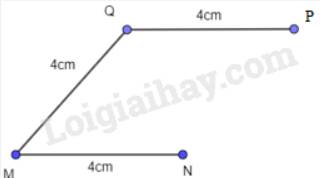
- Vẽ đoạn thẳng MN = 4 cm
- Vẽ đoạn thẳng MQ = 4 cm
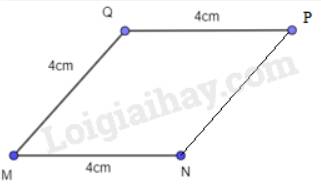
- Từ Q vẽ đường thẳng song song với MN, trên đường thẳng đó lấy điểm P sao cho PQ = 4 cm.
- Nối P với N ta được hình thoi MNPQ.

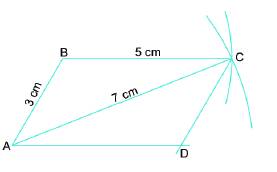
- Đặt một đầu compa tại điểm B đầu còn lại tại điểm C. Giữ nguyên compa và đặt một đầu tại điểm A, nếu đầu còn lại trùng với điểm D thì BC = AD.
- Đặt một đầu compa tại điểm B đầu còn lại tại điểm A. Giữ nguyên compa và đặt một đầu tại điểm C, nếu đầu còn lại trùng với điểm D thì AB = CD.
- Qua kiểm tra ta thấy BC = AD và AB = CD.

Câu 28. Tổ công tác Covid-19 của bệnh viện Đại học Y Dược gồm 90 bác sĩ và 84 y tá được phân công về 1 huyện để thực hiện xét thần tốc nhằm khoanh vùng dập dịch và điều trị Covid-19 trong các khu cách ly. Muốn phục vụ được nhiều xã hơn, đội dự định chia thành các tổ sao cho số bác sĩ và y tá của các tổ bằng nhau. Hỏi có thể chia được nhiều nhất thành bao nhiêu tổ? Mỗi tổ có mấy bác sĩ, mấy y tá?
A. 12 tổ; 6 bác sĩ và 5 y tá. B. 12 tổ; 5 bác sĩ và 6 y tá.
C. 6 tổ; 15 bác sĩ và 14 y tá. D. 6 tổ; 14 bác sĩ và 15 y tá.

a) AB=CD; BC=AD.
b) Hai cặp cạnh AB và CD song song với nhau, BC và AD song song với nhau.
c) Sử dụng thước đo các cạnh ta thấy OA=OC; OB=OD.

Tham khảo:
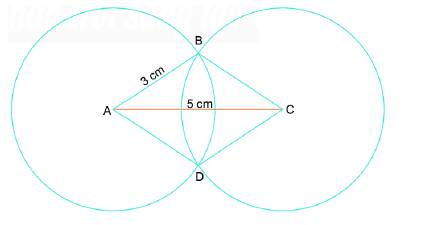
- Vẽ đoạn thẳng AC =5 cm.

- Lấy A và C là tâm, vẽ hai đường tròn bán kính 3 cm (hình vẽ), hai đường tròn này cắt nhau tại hai điểm B và D.
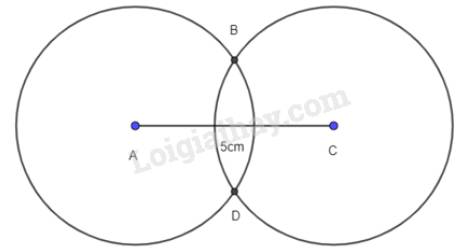
- Nối B với A, B với C, D với C.



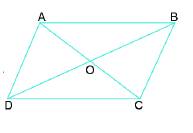
a)Xét 2 tam giác AOB và DOC
- BO=OD ( GT )
- AO=OC (gt)
- \(\widehat{AOB}=\widehat{DOC}\)(hai góc dối đỉnh)
=>tam giac AOB = tam giac DOC
b)Tự vẽ hình
Vì tam giác AOB=tam giác COD
\(\Rightarrow\)góc B=góc D(2 góc tương ứng)
Mà góc B và góc D ở vị trí SLT nên AB song song với CD
Tham khảo:
Cách 1:
Vẽ đoạn thẳng AC = 5 cm.
Lấy trung điểm O của AC.
Qua O kẻ đoạn thẳng BD =7cm (B và D khác phía nhau so với AC) sao cho O là trung điểm của BD (tức là OB=OD=3,5cm).
Nối A với B, A với D, B với C, C với D ta được hình bình hành ABCD.
Sử dụng thước đo các cạnh ta thấy AB=CD, AD=BC.
Hình vừa vẽ sử dụng tính chất hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.
Cách 2:
Vẽ đoạn thẳng AC = 5 cm.
Lấy trung điểm O của đoạn thẳng AC. Vẽ đường tròn tâm O bán kính 3,5 cm.
Vẽ đường thẳng đi qua tâm O cắt đường tròn tại hai điểm B và D.
Nối A với B, B với C, C với D, D với A, ta được hình bình hành ABCD.