Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = b\sqrt 2 \)
\(\cos \widehat {SCA} = \frac{{AC}}{{SC}} = \frac{1}{2} \Rightarrow \widehat {SCA} = {60^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {60^ \circ }\)
Chọn A.

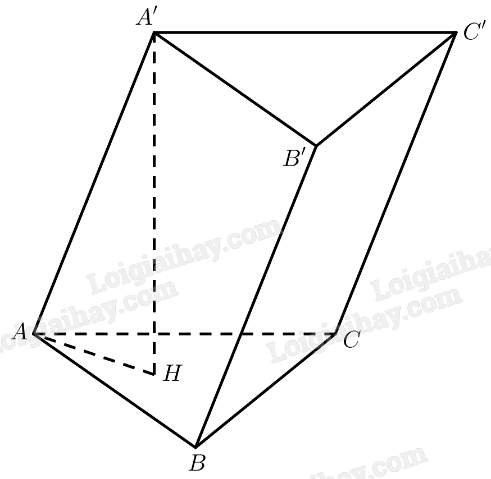
Gọi \(H\) là hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\)
\(\begin{array}{l} \Rightarrow A'H \bot \left( {ABC} \right)\\ \Rightarrow \left( {AA',\left( {ABC} \right)} \right) = \left( {AA',AH} \right) = \widehat {A'AH}\end{array}\)
\(\Delta AA'H\) vuông tại \(H \Rightarrow A'H = AA'.\sin \widehat {A'AH} = \frac{{a\sqrt 3 }}{2}\)
Vì \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\) nên \(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = d\left( {A',\left( {ABC} \right)} \right) = A'H = \frac{{a\sqrt 3 }}{2}\)

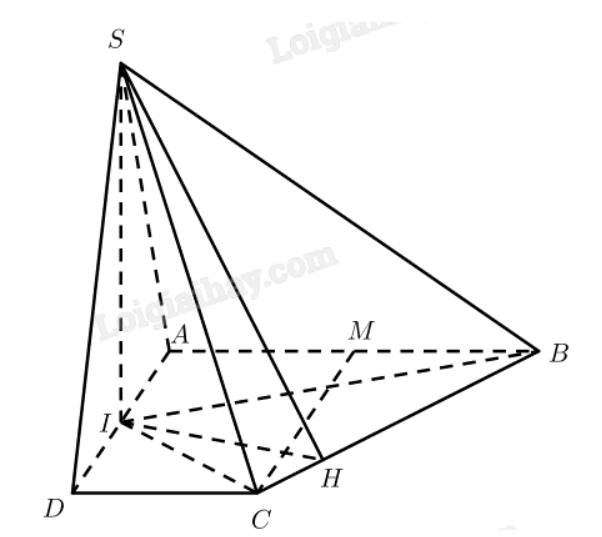
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)

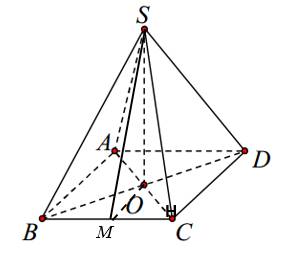
Gọi \(M\) là trung điểm \(BC\).
Ta có:\(OM=\dfrac{1}{2}.AB=2a;AC=\sqrt{AB^2+BC^2}=5a;OC=\dfrac{1}{2}AC=\dfrac{5}{2}a\)
\(SO=\sqrt{SC^2-OC^2}=\dfrac{5\sqrt{3}}{2}a\)
\(\left[S,BC,A\right]=\widehat{SMO}\)
\(\tan\widehat{SMO}=\dfrac{SO}{OM}=\dfrac{5\sqrt{3}}{4}\)
Suy ra:\(\widehat{SMO}=65,2^o\)
\(\Rightarrow D\)

16.
Đặt cạnh của đáy là x
\(DM=\sqrt{AD^2+AM^2}=\sqrt{x^2+\left(\frac{x}{2}\right)^2}=\frac{x\sqrt{5}}{2}\)
\(CM=\sqrt{BC^2+BM^2}=\sqrt{x^2+\left(\frac{x}{2}\right)^2}=\frac{x\sqrt{5}}{2}\)
\(\Rightarrow DM=CM\Rightarrow\Delta_vSMD=\Delta_vSMC\)
\(\Rightarrow SC=SD=2a\sqrt{5}\)
Mà \(SM\perp\left(ABCD\right)\Rightarrow\widehat{SCM}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCM}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}CM=SC.cos60^0=a\sqrt{5}\\SM=SC.sin60^0=a\sqrt{15}\end{matrix}\right.\) \(\Rightarrow AB=x=\frac{2CM}{\sqrt{5}}=2a\)
Gọi N là trung điểm CD \(\Rightarrow CD\perp\left(SMN\right)\)
\(AM//CD\Rightarrow AM//\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(M;\left(SCD\right)\right)\)
Từ M kẻ \(MM\perp SN\Rightarrow MH\perp\left(SCD\right)\Rightarrow MH=d\left(H;\left(SCD\right)\right)\)
\(MN=AB=2a\)
\(\frac{1}{MH^2}=\frac{1}{SM^2}+\frac{1}{MN^2}\Rightarrow MH=\frac{SM.MN}{\sqrt{SM^2+MN^2}}=\frac{2a\sqrt{15}}{\sqrt{19}}\)
14.
Do \(\widehat{C'BC}\) là góc giữa (ABCD) và (ABC') nên \(\widehat{C'BC}=60^0\)
\(\Rightarrow CC'=BC.tan60^0=a\sqrt{3}\)
15.
Gọi H là trung điểm BC \(\Rightarrow OH\perp BC\)
Chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOH\right)\)
Từ O kẻ \(OK\perp SH\Rightarrow OK\perp\left(SBC\right)\Rightarrow OK=d\left(O;\left(SBC\right)\right)\)
\(OH=\frac{1}{2}AB=\frac{a}{2}\) ; \(AC=a\sqrt{2}\Rightarrow OA=\frac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2-OA^2}=\frac{a\sqrt{2}}{2}\)
\(\frac{1}{OK^2}=\frac{1}{SO^2}+\frac{1}{OH^2}\Rightarrow OK=\frac{SO.OH}{\sqrt{SO^2+OH^2}}=\frac{a\sqrt{6}}{6}\)

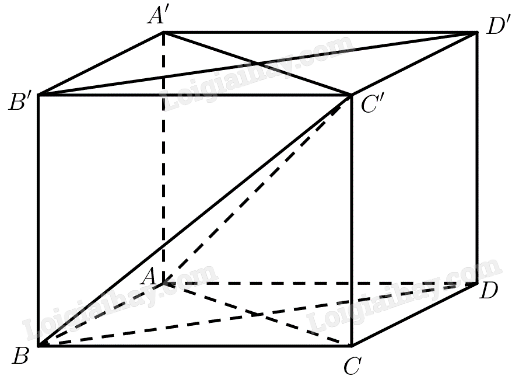
a) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(BB' \bot \left( {ABCD} \right) \Rightarrow BB' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {B{\rm{DD'B'}}} \right)\\AC \subset \left( {ACC'A'} \right)\end{array} \right\} \Rightarrow \left( {ACC'A'} \right) \bot \left( {B{\rm{DD}}'B'} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AB\parallel C{\rm{D}}\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C{\rm{D}}\parallel C'{\rm{D}}'\)
\( \Rightarrow AB\parallel C'{\rm{D}}' \Rightarrow d\left( {AB,C'{\rm{D}}'} \right) = d\left( {B,C'{\rm{D}}'} \right)\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow C'D' \bot B'C'\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C'D' \bot CC'\)
\( \Rightarrow C'D' \bot \left( {BCC'B'} \right) \Rightarrow C'D' \bot BC' \Rightarrow d\left( {B,C'{\rm{D}}'} \right) = BC'\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\begin{array}{l}CC' \bot \left( {ABCD} \right) \Rightarrow \left( {AC',\left( {ABCD} \right)} \right) = \left( {AC',AC} \right) = \widehat {CAC'} = {60^ \circ }\\ \Rightarrow CC' = AC.\tan \widehat {CAC'} = a\sqrt 6 \end{array}\)
\(\Delta BCC'\) vuông tại \(C \Rightarrow BC{'^2} = \sqrt {B{C^2} + CC{'^2}} = a\sqrt 7 \)
Vậy \(d\left( {AB,C'{\rm{D}}'} \right) = a\sqrt 7 \).

a)
\(38^\circ = \frac{{\pi .38}}{{180}} = \frac{{19\pi }}{{90}}\,\,\,\left( {rad} \right)\)
b)
\( - 115^\circ = \frac{{\pi .\left( { - 115} \right)}}{{180}} = \frac{{ - 23\pi }}{{36}}\,\,\left( {rad} \right)\)
c)
\({\left( {\frac{3}{\pi }} \right)^\circ }= \frac{{\pi .\frac{3}{\pi }}}{{180}} = \frac{1}{{60}}\,\,\,\left( {rad} \right)\)


Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).

a) Đáp án:B
b) Đáp án:D
c) Đáp án:B
d) Đáp án:B