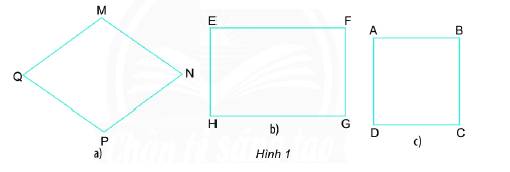
a) Quan sát các hình dưới (Hình 1) và cho biết hình nào là hình vuông.
b) Với hình vừa tìm được, hãy dùng thước và êke để kiểm tra xem các cạnh có bằng nhau không, các góc có bằng nhau không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chỉ có ABC là hình có 3 cạnh bằng nhau.
b) Các góc của tam giác ABC bằng nhau và đều bằng \(60^\circ \) .

Đặt ê ke như hình vẽ để kiểm tra xem mỗi tứ giác có hay không hai cạnh song song.
+ Tứ giác ABCD có AB // CD nên là hình thang.
+ Tứ giác EFGH không có hai cạnh nào song song nên không phải hình thang.
+ Tứ giác KMNI có KM // IN nên là hình thang.

a) Các cạnh của hình thoi bằng nhau.
b) Kẻ đường thẳng qua B và vuông góc với BC. Đặt êke có góc vuông tại điểm cắt nhau giữa đường thẳng vừa kẻ và AD, đặt một cạnh góc vuông của êke trùng với đường thẳng ta thấy cạnh góc vuông còn lại của êke trùng khít với cạnh AD.
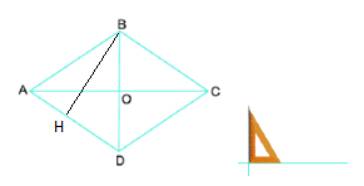
Khi đó BC và AD song song với nhau.
Tương tự AB và CD song song với nhau.
c) Tương tự như phần b, ta đặt đầu có góc vuông tại điểm O, đặt một cạnh góc vuông trùng với OB thì cạnh góc vuông còn lại trùng với OC hoặc OA. Khi đó AC và BD vuông góc với nhau.
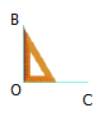

1) Dùng thước thẳng hoặc compa, ta được: AB = BC = CD = AD. Vậy các cạnh của hình thoi bằng nhau.
2) Dùng eke ta thấy AC vuông góc với BD. Vậy hai đường chéo của hình thoi vuông góc với nhau.
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình thoi song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình thoi ABCD bằng nhau.

tham khảo:
Ta dùng êke để kiểm tra từng mặt phẳng tấm gỗ có vuông góc với trụ chống không. Nếu có thì các tấm gỗ này song song với nhau

Dùng thước ta thấy các đoạn thẳng MN = NP = PQ = QM.
Dùng êke ta thấy các góc M, N, P, Q bằng nhau.
Như vậy, hình MNPQ cho trong hình trên là hình vuông.

1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.

Sử dụng êke đo góc và thấy 4 góc không vuông nên đây không là hình vuông.
Vậy bạn Trang nói sai.

- Dùng êke đặt phần có góc vuông tại điểm O đặt một cạnh góc vuông của êke trùng với OI khi đó cạnh góc vuông còn lại trùng với OJ. Vậy IK và JL vuông góc với nhau.
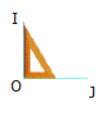
- Dùng compa đặt một đầu của compa tại điểm O. Đầu còn lại đặt tại điểm I. Giữa nguyên đầu tại điểm O và di chuyển đầu tại điểm I, thấy đầu đó trùng với các điểm J, K, L. Vậy OI = OJ = OK = OL. Hay hai đường chéo IK và JL cắt nhau tại trung điểm của mỗi đường.
a) Hình c là hình vuông.
b) Các cạnh của ABCD bằng nhau và các góc bằng nhau và bằng \(90^\circ \).