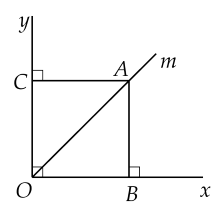
Cho $\widehat{xOy}={{90}^{\circ}}$ và tia phân giác $Om$. Lấy điểm $A$ trên $Om.$ Kẻ $AB, \, AC$ lần lượt vuông góc với $Ox, \, Oy\,.$ Chứng minh $OBAC$ là hình vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔOIA vuông tại I và ΔOIB vuông tại I có
OI chung
IA=IB
=>ΔOIA=ΔOIB
=>OA=OB
=>ΔOAB cân tại O
2: OA+AM=OM
OB+BN=ON
mà OA=OB và AM=BN
nên OM=ON
=>ΔOMN cân tại O
Xét ΔOMN có OA/OM=OB/ON
nên AB//MN

1: Xét ΔOAI vuông tại I và ΔOBI vuông tại I có
OI chung
góc AOI=góc BOI
=>ΔOAI=ΔOBI
=>OA=OB
=>ΔOAB cân tại O
2: OA+AM=OM
OB+BN=ON
mà OA=OB và AM=BN
nên OM=ON
Xét ΔOMN có OA/OM=OB/ON
nên AB//MN
3: góc NOK=180 độ
=>góc NOA+góc KOA=180 độ
=>góc KOA=180 độ-góc NOA=2(90 độ-góc IOA)=2*góc HOA
=>OH là phân giác của góc AOK

a: Xét ΔOAK vuông tại K và ΔOAH vuông tại H có
OA chung
\(\widehat{KOA}=\widehat{HOA}\)
Do đó: ΔOAK=ΔOAH
Suy ra: AK=AH
Câu b đề yêu cầu gì?

Xét ΔOMA vuông tại M và ΔOMB vuông tại M có
OA=OB
OM chung
Do đó: ΔOMA=ΔOMB
\(AC\perp Oy\) (gt); \(Ox\perp Oy\) (gt) => AC//Oy => AC//OB
C/m tương tự có AB//OC
=> OBAC là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{xOy}=90^o\)
=> OBAC là HCN
Ta có
AC=AB (Tính chất đường phân giác)
=> OBAC là hình vuông
Tứ giác ����OBAC có ba góc vuông: góc B= góc C = góc BOC= 90 độ �^=�^=���^=90∘==
∘
Nên ����OBAC là hình chữ nhật.
Mà �A nằm trên tia phân giác ��OM suy ra ��=��AB=AC.
Khi đó ����OBAC là hình vuông.