Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng \(\Delta \) ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng).a) Viết phương trình của đường thẳng \(\Delta \).b) Giao điểm của đường thẳng \(\Delta \) với trục tung trong tình...
Đọc tiếp
Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng \(\Delta \) ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng).
a) Viết phương trình của đường thẳng \(\Delta \).
b) Giao điểm của đường thẳng \(\Delta \) với trục tung trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.
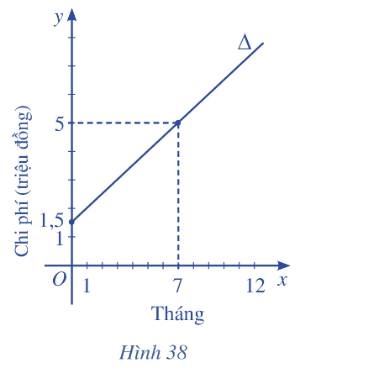
a) Đường thẳng \(\Delta \) đi qua hai điểm lần lượt có tọa độ \(\left( {0;1,5} \right),\left( {7;5} \right)\) nên \(\Delta \) có phương trình là:
\(\frac{{x - 0}}{{7 - 0}} = \frac{{y - 1,5}}{{5 - 1,5}} \Leftrightarrow \frac{x}{7} = \frac{{y - 1,5}}{{3,5}} \Leftrightarrow x - 2y + 3 = 0\)
b) Giao điểm của đường thẳng \(\Delta \) với trục \(Oy\) ứng với \(x = 0\). Thời điểm \(x = 0\)cho biết khoản phí tham gia ban đầu mà người tập phải trả. Khi \(x = 0\) thì \(y = 1,5\) , vì vậy khoản phí tham gia ban đầu mà người tập phải trả là 1 500 000 đồng.
c) 12 tháng đầu tiên ứng với \(x = 12\)
Từ phương trình đường thẳng \(\Delta \) ta có: \(x - 2y + 3 = 0 \Leftrightarrow y = \frac{1}{2}x + \frac{3}{2}\)
Thay \(x = 12\) vào phương trình đường thẳng ta có: \(y = \frac{1}{2}.12 + \frac{3}{2} = 7.5\)
Vậy tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục trong 12 tháng là 7tr5 nghìn đồng.