Question

[Quoc Tran Anh Le]

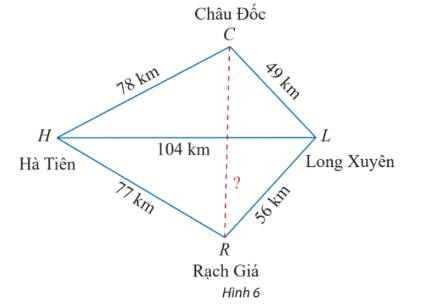
Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

Answer 1

[Hà Quang Minh]

Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:

\(\begin{array}{l}\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}} = \frac{{{{78}^2} + {{104}^2} - {{49}^2}}}{{2.78.104}} = \frac{{4833}}{{5408}}\\ \Rightarrow \;\widehat {CHL} \approx {26^o}39'40,05''\end{array}\)

Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:

\(\begin{array}{l}\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - L{R^2}}}{{2.HL.HR}} = \frac{{{{104}^2} + {{77}^2} - {{56}^2}}}{{2.104.77}} = \frac{{13609}}{{16016}}\\ \Rightarrow \;\widehat {LHR} \approx {31^o}49'10,4''\\ \Rightarrow \;\widehat {CHR} \approx {58^o}28'50,45''\end{array}\)

Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)

\(\begin{array}{l} \Leftrightarrow C{R^2} = {78^2} + {77^2} - 2.78.77\cos {58^o}28'50,45''\\ \Rightarrow CR \approx 75,72\end{array}\)

Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.