Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐỈnh: C, H, R, L
Đường chéo: CR, HL
Cạnh: CH, HR, RL, CL

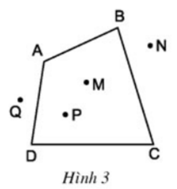
a) Hai đỉnh kề nhau: A và B, B và C, C và D, D và A
Hai đỉnh đối nhau: A và C, B và D
b) Đường chéo (đoạn thẳng nối hai đỉnh đối nhau): AC, BD
c) Hai cạnh kề nhau: AB và BC, BC và CD, CD và DA, DA và AB
Hai cạnh đối nhau: AB và CD, AD và BC
d) Góc: ∠A , ∠B , ∠C , ∠D
Hai góc đối nhau: ∠A và ∠C , ∠B và ∠D
e) Điểm nằm trong tứ giác (điểm trong của tứ giác): M, P
Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác): N, Q

Lời giải:
Gọi hình thoi là $ABCD$ có $AC=12, BD=8$ (cm)
Trung điểm của $AB,AD,CD,CB$ lần lượt là $M,N,P,Q$
Dễ thấy:
$MQ, NP\parallel AC$ và $MQ=NP=\frac{AC}{2}=6$ (cm)
$NM, QP\parallel BD$ và $MN=QP=\frac{BD}{2}=4$ (cm)
Mà $BD\perp AC$ (tính chất hình thoi)
$\Rightarrow (MQ\parallel NP)\perp (MN\parallel QP)$
$\Rightarrow MNPQ$ là hình chữ nhật
$S_{MNPQ}=MN.NP=4.6=24$ (cm2)

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(1)
Xét ΔCDA có
P là trung điểm của CD
Q là trung điểm của DA
Do đó: PQ là đường trung bình của ΔCDA
Suy ra: PQ//AC và \(PQ=\dfrac{AC}{2}\left(2\right)\)
Từ (1) và (2)suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành
a) QQ là trung điểm của ADAD
MM là trung điểm của ABAB
⇒QM⇒QM là đường trung bình của ΔABDΔABD
⇒QM∥=12BD⇒QM∥=12BD (1)
Tương tự PNPN là đường trung bình của ΔBCDΔBCD
⇒PN∥=12BD⇒PN∥=12BD (2)
Từ (1) và (2) suy ra QM∥=PN(∥=12BD)QM∥=PN(∥=12BD)
⇒⇒ tứ giác MNPQMNPQ là hình bình hành.
Ta có: QQ là trung điểm của ADAD
JJ là trung điểm của ACAC
⇒QJ⇒QJ là đường trung bình của ΔACDΔACD
⇒QJ∥=12CD⇒QJ∥=12CD (1)
Tương tự KNKN là đường trung bình của ΔBCDΔBCD
⇒KN∥=12CD⇒KN∥=12CD (2)
Từ (1) và (2) suy ra QJ∥=KN(∥=12CD)QJ∥=KN(∥=12CD)
⇒⇒ tứ giác JNKQJNKQ là hình bình hành.
b) Tứ giác MNPQMNPQ là hình bình hành
⇒ Gọi MP∩QN=O⇒ Gọi MP∩QN=O
⇒O⇒O là trung điểm của MPMP và QNQN
Tứ giác INKQINKQ là hình bình hành
Có hai đường chéo là QNQN và KJKJ
OO là trung điểm của QNQN
⇒O⇒O là trung điểm của KJKJ
⇒MP,NQ,JK⇒MP,NQ,JK đồng quy tại OO trung điểm của mỗi đường.

a) Các cạnh kề của \(BD\) là: \(BQ\), \(DN\)
Cạnh đối của cạnh \(BD\) là: \(NQ\)
b) Các đường chéo của tứ giác là: \(BN;\;DQ\)