Trong Hình 4.29, hai tam giác nào bằng nhau?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Cặp tam giác bằng nhau là:
\(\Delta ABC = \Delta MNP\) vì
\(\begin{array}{l}\widehat B = \widehat N( = 50^\circ )\\BC = NP\\\widehat C = \widehat P( = 70^\circ )\end{array}\)
Vậy \(\Delta ABC = \Delta MNP\) (g-c-g)
TT
1
28 tháng 1 2022
phải có hình hoặc số đo cạnh hoặc góc thì mới so sánh đc chứ
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
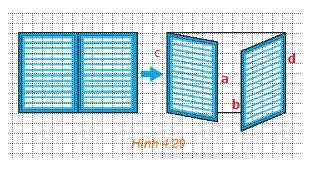
Vì a//c, b//d (do cánh cửa là hình chữ nhật)
Mà c//d.
Suy ra, a//b.
Do đó, hai mép ngoài của chúng luôn song song với nhau.
Nếu hai cánh cửa sổ có dạng hình thang như Hình 4.30, hai cánh cửa để hai mép ngoài của chúng song song với nhau khi cả hai cánh cửa được khép lại.
3 tháng 11 2016
tam giác ABC và tam giác HIK . vì AB = KI , góc B = góc K .
suy ra : AC=IH ; BC = KH
CM
20 tháng 9 2017
a) Mệnh đề Đúng.
Giả sử có ΔABC = ΔA’B’C’
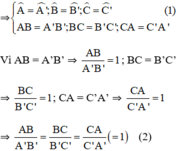
Từ (1) và (2) suy ra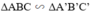 
b) Mệnh đề Sai.
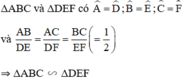
nhưng ΔABC và ΔDEF không bằng nhau
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Khẳng định đúng là a, khẳng định sai là b.
- Khẳng định a đúng vì
Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
- Khẳng định b sai vì
Nếu\(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) thì tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi \(k \ne 1\) thì \(AB \ne A'B';AC \ne A'C';BC \ne B'C'\) nên hai tam giác không bằng nhau.
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)