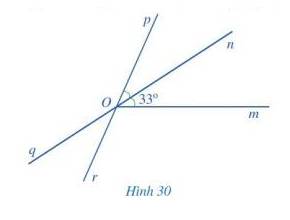
Trong Hình 30, tính số đo của \(\widehat {mOp};\widehat {qOr};\widehat {pOq}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
1
KV
19 tháng 8 2023
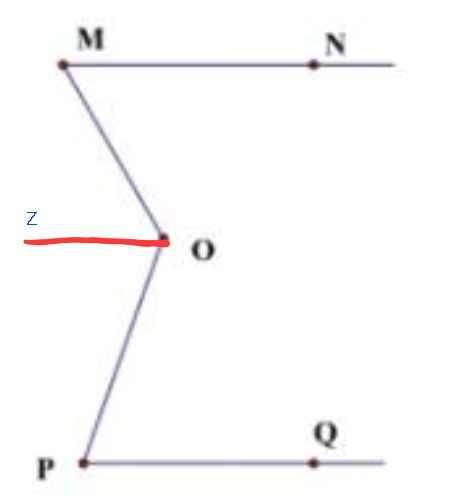Vẽ tia Oz //MN
⇒ ∠MOz = ∠OMN = 60⁰
⇒ ∠zOP = ∠MOP - ∠MOz
= 130⁰ - 60⁰
= 70⁰
Để MN // PQ thì MN // Oz
⇒ ∠P = ∠OPQ = ∠POz = 70⁰ (so le trong)
4 tháng 5 2020
\(\widehat{XOM}\)= \(150^o\)
\(\widehat{XON}\) = \(30^o\)
Nên góc \(\widehat{MON}\) = \(\widehat{XOM}\) - \(\widehat{XON}\) = \(150^o\)- \(30^o\) = \(120^o\) Tia Oy là tia phân giác của góc \(\widehat{MOP}\)
VÌ tia Oy nằm giữa hai tia Om và Op , có chung một độ là \(30^o\) CHÚC BẠN THÀNH CÔNG
T
25 tháng 6 2020
a. Ta có ; \(\widehat{mOn}=\widehat{xOm}-\widehat{xOn}\)
\(\Rightarrow\widehat{mOn}=150^o-30^o\)
\(\Rightarrow\widehat{mOn}=120^o\)
Vậy \(\widehat{mOn}=120^o\)
b . Ta có ; \(\widehat{yOm}=\widehat{xOy}-\widehat{xOm}\)
\(\Rightarrow\widehat{yOm}=180^o-150^o\)
\(\Rightarrow\widehat{yOm}=30^o\) \((1)\)
Mặt khác ; \(\widehat{yOp}=\widehat{xOn}\)\((\)đối đỉnh \()\)
mà bài cho \(\widehat{xOn}=30^o\)
\(\Rightarrow\widehat{yOp}=30^o\)\((2)\)
Từ \((1)\)và \((2)\)suy ra ;
\(\widehat{yOm}=\widehat{yOp}=30^o\)
\(\Rightarrow\)tia Oy là tia phân giác của \(\widehat{mOp}\)
Học tốt
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
Ta chia tứ giác ABCD thành tam giác ACD và tam giác ABC
\( \Rightarrow \) Số đo tổng các góc tam giác ACD = tổng số đo các góc tam giác ABC = \({180^o}\)
\( \Rightarrow \)Tổng số đo các góc trong tứ giác ABCD = tổng số đo các góc 2 tam giác ACD và ABC \( = {2.180^o} = {360^o}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
LH
20 tháng 4 2017
Ta có tam giác ABC vuông ở A nên
\(\widehat{ABC}+\widehat{C}_1=90^0\)
Trong đó tam giác OCD vuông ở D có \(\widehat{MOP}=\widehat{C}_2=90^0\)
Nên \(\widehat{MOP}=\widehat{ABC}\)
\(\widehat{MOP}=32^0\)
20 tháng 4 2017
Ta có tam giác ABC vuông ở A nên ∠ABC + ∠BCA = 900
Trong đó tam giác OCD vuông ở D có ∠COD + ∠OCD = 900
mà góc ∠BCA = ∠OCD ( 2 góc đối đỉnh)
Từ (1),(2),(3) ∠COD = ∠ABC mà ∠ABC= 320 . Nên ∠COD = 320
hay chính là ∠MOP =320
AD
6 tháng 2 2021
a)Có :\(\widehat{MOP}+\widehat{PON}=\widehat{MON}\)
\(\Rightarrow\widehat{MOP}+70^o=155^o\)
\(\Rightarrow\widehat{MOP}=85^o\)
b) Có :\(\widehat{QOM}+\widehat{MON}=180^o\)
\(\Rightarrow\widehat{QOM}+155^o=180^o\)
\(\Rightarrow\widehat{QOM}=25^o\)
A
0
Vì On là tia phân giác của \(\widehat {mOp}\) nên:
+) \(\widehat {pOn}= \widehat {mOn}=33^\circ \)
+) \(\widehat {mOp} = 2.\widehat {mOn} = 2.33^\circ = 66^\circ \)
Vì \(\widehat {qOr} = \widehat {pOn}\) ( 2 góc đối đỉnh), mà \(\widehat {pOn} = 33^\circ \Rightarrow \widehat {qOr} = 33^\circ \)
Vì \(\widehat {pOq} + \widehat {qOr} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {pOq} + 33^\circ = 180^\circ \Rightarrow \widehat {pOq} = 180^\circ - 33^\circ = 147^\circ \)
Vậy \(\widehat {mOp} = 66^\circ ;\widehat {qOr} = 33^\circ ;\widehat {pOq} = 147^\circ \)