Tìm giá trị của:
\(\begin{array}{l}a)\sqrt {1600} ;\\b)\sqrt {0,16} ;\\c)\sqrt {2\frac{1}{4}} \end{array}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\begin{array}{l}a)\sqrt {0,49} + \sqrt {0,64} = 0,7 + 0,8 = 1,5;\\b)\sqrt {0,36} - \sqrt {0,81} = 0,6 - 0,9 = - 0,3;\\c)8.\sqrt 9 - \sqrt {64} = 8.3 - 8 = 24 - 8 = 16;\\d)0,1.\sqrt {400} + 0,2.\sqrt {1600} = 0,1.20 + 0,2.40 = 2 + 8 = 10\end{array}\)

a) Tìm tập xác định của hàm số trên.
\(f\left( x \right)\) có nghĩa khi x0.
=> Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
b) Tính giá trị của hàm số khi \(x = - 1;x = 2022\)
Với \(x = - 1\), suy ta \(x < 0\)\( \Rightarrow y = - x = - \left( { - 1} \right) = 1\).
Với \(x = 2022\), suy ra \(x > 0\)\( \Rightarrow y = x = 2022\).

+ Biểu diễn miền nghiệm của BPT \(x - y \le 6\)
Bước 1: Vẽ đường thẳng \(d:x - y = 6\) trên mặt phẳng tọa độ Õy
Bước 2: Lấy O(0;0) không thuộc d, ta có: \(0 - 0 = 0 \le 6\) => điểm O(0;0) thuộc miền nghiệm
=> Miền nghiệm của BPT \(x - y \le 6\) là nửa mp bờ d, chứa gốc tọa độ.
+ Tương tự, ta có miền nghiệm của BPT \(2x - y \le 2\) là nửa mp bờ \(d':2x - y = 0\), chứa gốc tọa độ.
+ Miền nghiệm của BPT \(x \ge 0\) là nửa mp bên phải Oy (tính cả trục Oy)
+ Miền nghiệm của BPT \(y \ge 0\) là nửa mp phía trên Ox (tính cả trục Ox)
Biểu diễn trên cùng một mặt phẳng tọa độ và gạch bỏ các miền không là nghiệm của từng BPT, ta được:
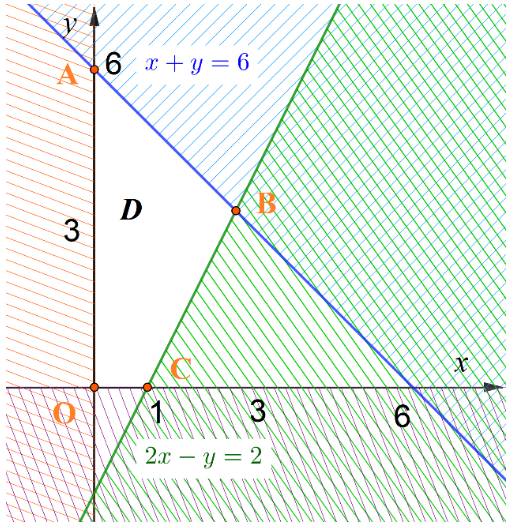
Miền nghiệm của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch) với \(A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\)
b)
Thay tọa độ các điểm \(O(0;0),A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\) và biểu thức \(F(x;y) = 2x + 3y\) ta được:
\(\begin{array}{l}F(0;0) = 2.0 + 3.0 = 0\\F(0;6) = 2.0 + 3.6 = 18\\F(\frac{8}{3};\frac{{10}}{3}) = 2.\frac{8}{3} + 3.\frac{{10}}{3} = \frac{{46}}{3}\\F(1;0) = 2.1 + 3.0 = 2\end{array}\)
\( \Rightarrow \min F = 0\), \(\max F = 18\)
Vậy trên miền D, giá trị nhỏ nhất của F bằng 0, giá trị lớn nhất của F bằng \(18\).

\(\begin{array}{l}a)\sqrt x - 16 = 0\\\sqrt x = 16\\x = {16^2}\\x = 256\end{array}\)
Vậy x = 256
\(\begin{array}{l}b)2\sqrt x = 1,5\\\sqrt x = 1,5:2\\\sqrt x = 0.75\\x = {(0,75)^2}\\x = 0,5625\end{array}\)
Vậy x = 0,5625
\(\begin{array}{l}c)\sqrt {x + 4} - 0,6 = 2,4\\\sqrt {x + 4} = 2,4 + 0,6\\\sqrt {x + 4} = 3\\x + 4 = 9\\x = 5\end{array}\)
Vậy x = 5

Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0).
Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(y - 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.
Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4).
Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.
Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1).
Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.
Bước 4: Vẽ đường thẳng \(d_4: x + y = - 1\) đi qua (-1;0) và (0;-1).
Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(x + y \ge - 1\) là nửa mp bờ \(d_4\), chứa điểm O.
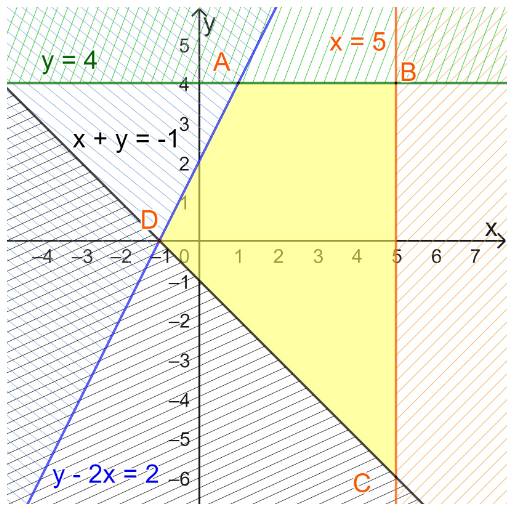
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với
A(1;4); B(5;4), C(5;-6); D(-1;0).
Giá trị F tại các điểm A, B, C, D lần lượt là:
\(F\left( {1;4} \right) = - 1 - 4 = - 5\)
\(F\left( {5;4} \right) = - 5 - 4 = - 9\)
\(F\left( {5;-6} \right) = - 5 - (-6) = 1\)
\(F\left( { - 1;0} \right) = - \left( { - 1} \right) - 0 = 1\)
Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.

\(\begin{array}{l}a)\frac{x}{{ - 3}} = \frac{7}{{0,75}}\\ \Rightarrow x.0,75 = ( - 3).7\\ \Rightarrow x = \frac{{( - 3).7}}{{0,75}} = - 28\end{array}\)
Vậy x = 28
\(\begin{array}{l}b) - 0,52:x = \sqrt {1,96} :( - 1,5)\\ - 0,52:x = 1,4:( - 1,5)\\ x = \dfrac{(-0,52).(-1,5)}{1,4}\\x = \frac{39}{{70}}\end{array}\)
Vậy x = \(\frac{39}{{70}}\)
\(\begin{array}{l}c)x:\sqrt 5 = \sqrt 5 :x\\ \Leftrightarrow \frac{x}{{\sqrt 5 }} = \frac{{\sqrt 5 }}{x}\\ \Rightarrow x.x = \sqrt 5 .\sqrt 5 \\ \Leftrightarrow {x^2} = 5\\ \Leftrightarrow \left[ {_{x = - \sqrt 5 }^{x = \sqrt 5 }} \right.\end{array}\)
Vậy x \( \in \{ \sqrt 5 ; - \sqrt 5 \} \)
Chú ý:
Nếu \({x^2} = a(a > 0)\) thì x = \(\sqrt a \) hoặc x = -\(\sqrt a \)
a: \(\dfrac{x}{-3}=\dfrac{7}{0.75}=\dfrac{28}{3}\)
=>\(x=\dfrac{28\left(-3\right)}{3}=-28\)
b: \(-\dfrac{0.52}{x}=\dfrac{\sqrt{1.96}}{-1.5}=\dfrac{1.4}{-1.5}\)
=>\(x=0.52\cdot\dfrac{1.5}{1.4}=\dfrac{39}{70}\)
c: \(\dfrac{x}{\sqrt{5}}=\dfrac{\sqrt{5}}{x}\)
=>\(x^2=5\)
=>\(x=\pm\sqrt{5}\)

Tham khảo:
+) Dễ thấy: hàm số được xác định với mọi \(x > 0\) và \(x < 0\).
Do đó tập xác định của hàm số là \(D = \mathbb{R}{\rm{\backslash }}\{ 0\} \)
+) Với \(x \in D\):
+ Nếu \(x > 0\) thì \(f(x) = 1\)
+ Nếu \(x < 0\) thì \(f(x) = - 1\)
Vậy tập giá trị của hàm số là \(T = \{ - 1;1\} \)
+) Vẽ đồ thị hàm số:
Với \(x \in ( - \infty ;0)\) đồ thị hàm số là đường thẳng \(y = - 1\)
Với \(x \in (0; + \infty )\) đồ thị hàm số là đường thẳng \(y = 1\)
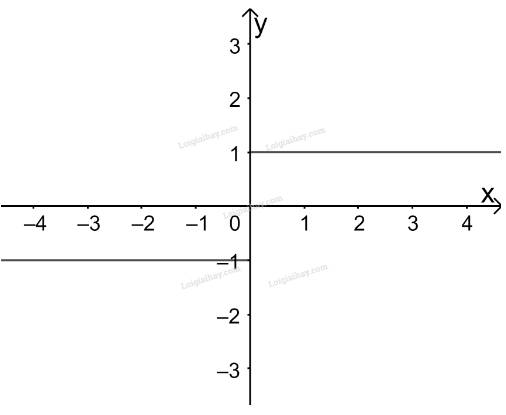
Ta được đồ thị hàm số như hình trên.

\(\begin{array}{l}a)A = (2 - \frac{1}{2} - \frac{1}{8}):(1 - \frac{3}{2} - \frac{3}{4})\\ = (\frac{{16}}{8} - \frac{4}{8} - \frac{1}{8}):(\frac{4}{4} - \frac{6}{4} - \frac{3}{4})\\ = \frac{{11}}{8}:\frac{{ - 5}}{4}\\ = \frac{{11}}{8}.\frac{4}{{ - 5}}\\ = \frac{{ - 11}}{{10}}\\b)B = 5 - \frac{{1 + \frac{1}{3}}}{{1 - \frac{1}{3}}}\\ = 5 - \frac{{\frac{3}{3} + \frac{1}{3}}}{{\frac{3}{3} - \frac{1}{3}}}\\ = 5 - \frac{{\frac{4}{3}}}{{\frac{2}{3}}}\\ = 5 - \frac{4}{3}:\frac{2}{3}\\ = 5 - \frac{4}{3}.\frac{3}{2}\\ = 5 - 2\\ = 3\end{array}\)
Chú ý:
Khi thực hiện phép cộng hai phân số, nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.

a) Với a = 0, tại x = 4, ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2.0 + 1 = 1\\ \Rightarrow \mathop {\lim }\limits_{x \to 4} f\left( x \right) \ne f\left( 4 \right)\end{array}\)
Do đó hàm số không liên tục tại x = 4.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2a + 1\end{array}\)
Để hàm số liên tục tại x = 4 thì \(\mathop {\lim }\limits_{x \to 4} f\left( x \right) = f\left( 4 \right)\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;21{\rm{ }} = {\rm{ }}2a{\rm{ }} + {\rm{ }}1}\\{ \Leftrightarrow \;2a{\rm{ }} = {\rm{ }}20}\\{ \Leftrightarrow \;a{\rm{ }} = {\rm{ }}10}\end{array}\)
Vậy với a = 10 thì hàm số liên tục tại x = 4.
c) TXĐ: \(\mathbb{R}\)
Với \(x\; \in \;\left( {-{\rm{ }}\infty ;{\rm{ }}4} \right)\) có \(f\left( x \right) = {x^2} + x + 1\) liên tục với mọi x thuộc khoảng này.
Với \(x\; \in \;\left( {4;{\rm{ }} + \infty } \right)\) có \(f\left( x \right) = 2a + 1\) liên tục với mọi x thuộc khoảng này.
Do đó hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) khi hàm số \(f\left( x \right)\) liên tục tại điểm x = 4 khi a = 10.
Vậy với a = 10 hàm số liên tục trên tập xác định của nó.
\(\begin{array}{l}a)\sqrt {1600} = 40;\\b)\sqrt {0,16} = 0,4;\\c)\sqrt {2\frac{1}{4}} = \sqrt {\frac{9}{4}} = \frac{3}{2}\end{array}\)
\(\text{a)}\sqrt{1600}=40\)
\(\text{b)}\sqrt{0,16}=0,4\)
\(\text{c)}\sqrt{2\dfrac{1}{4}}=\sqrt{\dfrac{9}{4}}=\dfrac{3}{2}\)