Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy hàm số có nghĩa với mọi số thực nên \(D = \mathbb{R}\)
b)
Điều kiện: \(2 - 3x \ge 0 \Leftrightarrow x \le \frac{2}{3}\)
Vậy tập xác định: \(S = \left( { - \infty ;\frac{2}{3}} \right]\)
c) Điều kiện: \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
d) Ta thấy hàm số có nghĩa với mọi \(x \in \mathbb{Q}\) và \(x \in \mathbb{R}\backslash \mathbb{Q}\) nên tập xác định: \(D = \mathbb{R}\).

Tham khảo:
+) Dễ thấy: hàm số được xác định với mọi \(x > 0\) và \(x < 0\).
Do đó tập xác định của hàm số là \(D = \mathbb{R}{\rm{\backslash }}\{ 0\} \)
+) Với \(x \in D\):
+ Nếu \(x > 0\) thì \(f(x) = 1\)
+ Nếu \(x < 0\) thì \(f(x) = - 1\)
Vậy tập giá trị của hàm số là \(T = \{ - 1;1\} \)
+) Vẽ đồ thị hàm số:
Với \(x \in ( - \infty ;0)\) đồ thị hàm số là đường thẳng \(y = - 1\)
Với \(x \in (0; + \infty )\) đồ thị hàm số là đường thẳng \(y = 1\)
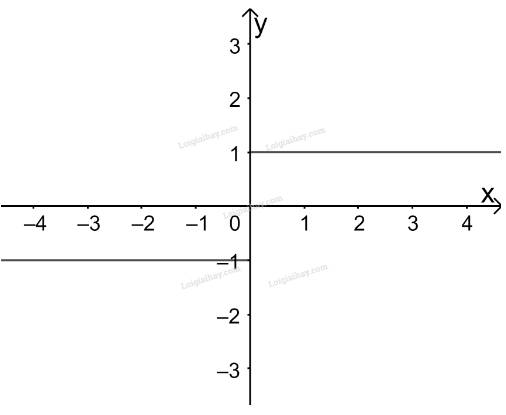
Ta được đồ thị hàm số như hình trên.

Tham khảo:
Hàm số \(f\left( x \right) = \left| x \right|\) xác định trên \(D = \mathbb{R}\)
Trên khoảng \(( - \infty ;0)\) ta vẽ đồ thị hàm số \(y = - x\), đi qua 2 điểm \(A( - 1;1),B( - 2;2)\)
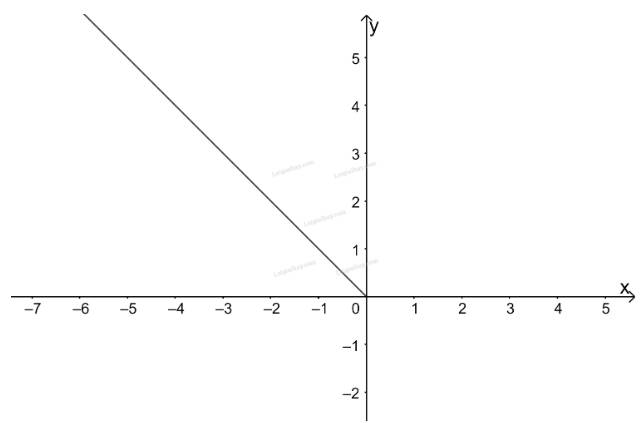
Trên khoảng \((0; + \infty )\) ta vẽ đồ thị hàm số \(y = x\), đi qua 2 điểm \(A'(1;1),B'(2;2)\)
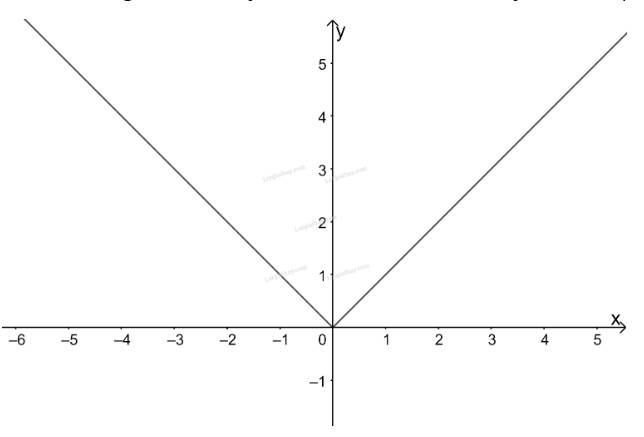
Như vậy ta được đồ thị hàm số \(f\left( x \right) = \left| x \right|\).

a: TXĐ: D=R
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)

Ta có: \(\overrightarrow {{u_1}} = \left( {1; - 2} \right) \Rightarrow \overrightarrow {{n_1}} = \left( {2;1} \right)\) và \(\overrightarrow {{u_2}} = \left( {1;3} \right) \Rightarrow \overrightarrow {{n_2}} = \left( {3; - 1} \right)\).
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {2.3 + 1.( - 1)} \right|}}{{\sqrt {{2^2} + {1^2}} .\sqrt {{3^2} + {{( - 1)}^2}} }} = \frac{{\sqrt 2 }}{2} \\ \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\)

a) Khoảng cách từ điểm A đến \({\Delta _1}\) là: \(d\left( {A,{\Delta _1}} \right) = \frac{{\left| {3.1 - 1.\left( { - 2} \right) + 4} \right|}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = \frac{9}{{\sqrt {10} }}\)
b) Phương trình tổng quát của đường thẳng \({\Delta _2}\)là: \(2x + y + 3 = 0\)
Khoảng cách từ điểm B đến \({\Delta _2}\) là: \(d\left( {A,{\Delta _2}} \right) = \frac{{\left| {2.\left( { - 3} \right) + 1.2 + 3} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{1}{{\sqrt 5 }}\)

Vì 4 đồ thị hàm số cắt trục tung tại 4 điểm phân biệt nên ta chỉ cần xác định tọa độ giao điểm của mỗi hàm số với trục tung là có thể phân biệt 4 đồ thị hàm số.
Đồ thị hàm số \(({P_1}):y = - 2{x^2} - 4x + 2\) cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2) => Đồ thị là đường màu xanh lá.
Đồ thị hàm số \(({P_2}):y = 3{x^2} - 6x + 5;\) cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5) => Đồ thị là đường màu xanh dương.
Đồ thị hàm số \(({P_3}):y = 4{x^2} - 8x + 7;\) cắt trục tung tại điểm có tung độ bằng 7, tức là đồ thị đi qua điểm có tọa độ (0; 7) => Đồ thị là đường màu nâu đỏ.
Đồ thị hàm số \(({P_4}):y = - 3{x^2} - 6x - 1\) cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1) => Đồ thị là đường màu vàng.

`C.x=2=>y=(2.2-3)/(2-1)=1=>Đ`
`D.x=1=>y=1^3-3=-2=>Đ`
`A.TXĐ:RR=>Đ`
`=>B.` sai

a) Tìm tập xác định của hàm số trên.
\(f\left( x \right)\) có nghĩa khi x0.
=> Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
b) Tính giá trị của hàm số khi \(x = - 1;x = 2022\)
Với \(x = - 1\), suy ta \(x < 0\)\( \Rightarrow y = - x = - \left( { - 1} \right) = 1\).
Với \(x = 2022\), suy ra \(x > 0\)\( \Rightarrow y = x = 2022\).