Quan sát Hình 3.
a) So sánh hệ số góc của hai đường thẳng:
\(d:y = 2x + 3\) và \(d':y = 2x - 2\).
Nêu nhận xét về vị trí giữa hai đường thẳng này.
b) Tìm đường thẳng \(d''\) đi qua gốc tọa độ \(O\) và song song với đường thẳng \(d\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Các đỉnh: A, B, C, D
Các cạnh: AB, BC, CD, DA
Các đường chéo: AC, BD
2) Độ dài các cạnh của hình vuông đều bằng nhau
Độ dài 2 đường chéo của hình vuông bằng nhau
3) Các góc của hình vuông đều bằng nhau và bằng 90o

1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.

1) Đỉnh: A, B, C, D
Đáy lớn: DC
Đáy nhỏ: AB
Đường chéo: AC, BD
Cạnh bên AD, BC
2) Dùng thước thẳng hoặc compa, ta đo được: AD = BC; AC = BD
Vậy: Hai cạnh bên hình thang cân bằng nhau
Hai đường chéo hình thang cân bằng nhau.
3) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
Vậy hai đáy của hình thang cân song song với nhau.
4) Hai góc kề một đáy của hình thang bằng nhau.

a)
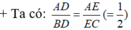
Nên theo định lí ta- let đảo ta có: DE // BC.
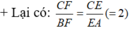
Nên theo định lí ta- let đảo ta có: EF // AB.
b) Tứ giác BDEF là hình bình hành vì có các cặp cạnh đối song song với nhau
c) Tứ giác BDEF là hình bình hành ⇒ DE = BF = 7
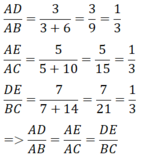
Ba cạnh của ΔADE tương ứng tỉ lệ với ba cạnh của ΔABC

1) Dùng thước thẳng hoặc compa, ta được: AB = BC = CD = AD. Vậy các cạnh của hình thoi bằng nhau.
2) Dùng eke ta thấy AC vuông góc với BD. Vậy hai đường chéo của hình thoi vuông góc với nhau.
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình thoi song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình thoi ABCD bằng nhau.

Gợi lên 2 tính chất:
- Hai đường thẳng vuông góc: Nếu 2 đường thẳng phân biệt cùng vuông góc với 1 mặt phẳng thì chúng song song với nhau
- Hai đường thẳng song song: Một đường thẳng vuông góc với một mặt phẳng thì sẽ vuông góc với tất cả các đường thẳng chứa trong mp đó

Ta có:
\(\begin{array}{l}a)\widehat {{O_1}} = 135^\circ ;\widehat {{O_3}} = 135^\circ \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\\b)\widehat {{O_2}} = 45^\circ ;\widehat {{O_4}} = 45^\circ \Rightarrow \widehat {{O_2}} = \widehat {{O_4}}\end{array}\)

b)
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).
a) Đường thẳng \(d:y = 2x + 3\) có hệ số góc là \(a = 2\).
Đường thẳng \(d':y = 2x - 2\) có hệ số góc là \(a' = 2\).
Hệ số góc của hai đường thẳng \(d\) và \(d'\) bằng nhau.
Từ đồ thị ta thấy, hai đường thẳng \(d\) và \(d'\) song song với nhau.
b) Đường thẳng \(d''\) đi qua gốc tọa độ \(O\) nên có dạng \(y = a''x\).
Từ đồ thị ta thấy, \(d''\) đi qua điểm \(\left( {1;2} \right)\) nên ta có:
\(2 = 1.a'' \Rightarrow a'' = 2\).
Do đó, đường thẳng \(d''\) là \(y = 2x\).