Cho ΔABC ( BAC = 90 °) đường cao AH, BC= 18cm, AC= 6 5cm. Từ H kẻ HI vuông góc với AB tại I. Qua A kẻ đường thẳng song song với BC cắt HI tại K a. Chứng minh s i n A K H + c o s K A C s i n A C H + c o s K H C =1 b. Tính độ dài đoạn thẳng HI và diện tích của tứ giác AIHC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
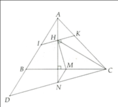

a: Bạn ghi lại đề nha bạn
b: ΔBAC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB=\sqrt{18^2-6.5^2}=\dfrac{7}{2}\sqrt{23}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH=\dfrac{281.75}{18}=\dfrac{1127}{72}\left(cm\right)\)
Xét ΔABC có HI//AC
nên \(\dfrac{HI}{AC}=\dfrac{BH}{BC}\)
=>\(\dfrac{HI}{6.5}=\dfrac{1127}{72}:18=\dfrac{1127}{1296}\)
=>\(HI\simeq5,65\left(cm\right)\)
ΔHAB vuông tại H có HI là đường cao
nên \(BI\cdot BA=BH^2\)
=>\(BI=\left(\dfrac{1127}{72}\right)^2:\dfrac{7}{2}\sqrt{23}=14,6\left(cm\right)\)
\(AI=AB-BI=3.5\sqrt{23}-14.6\simeq2,19\left(cm\right)\)
\(S_{AIHC}=\dfrac{1}{2}\left(HI+AC\right)\cdot AI\)
\(=\dfrac{1}{2}\cdot2.19\cdot\left(6.5+5.65\right)\simeq13,3\left(cm^2\right)\)