Cho góc x với cos x = \(-\dfrac{1}{2}\). Tính giá trị của biểu thức S= \(4\sin^{2_{ }}\)x + 8 tan2 x.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2021
\(P=sin^22x-\left[2sin\dfrac{x}{2}cos\dfrac{x}{2}\left(cos^4\dfrac{x}{2}-sin^4\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx\left(cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}\right)\left(cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx.cosx.1\right]^2\)
\(=sin^22x-\left[\dfrac{1}{2}sin2x\right]^2\)
\(=\dfrac{3}{4}sin^22x=\dfrac{3}{4}\left(1-cos^22x\right)=\dfrac{3}{4}\left(1-\dfrac{1}{4}\right)=\dfrac{9}{16}\)
NT
1
15 tháng 10 2023
\(B=cos^2x+sin^2x+tan^2x\)
\(=1+tan^2x\)
\(=\dfrac{1}{cos^2x}=1:\dfrac{1}{4}=4\)
HB
0
HP
6 tháng 8 2021
\(M=sinx.cosx+\dfrac{sin^2x}{1+cotx}+\dfrac{cos^2x}{1+tanx}\)
\(=sinx.cosx+\dfrac{sin^2x}{\dfrac{cosx+sinx}{sinx}}+\dfrac{cos^2x}{\dfrac{cosx+sinx}{cosx}}\)
\(=sinx.cosx+\dfrac{sin^3x+cos^3x}{cosx+sinx}\)
\(=sinx.cosx+\dfrac{\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{cosx+sinx}\)
\(=sinx.cosx+sin^2x+cos^2x-sinx.cosx\)
\(=sin^2x+cos^2x=1\)
10 tháng 9 2023
a: Ta sẽ có hình vẽ sau:
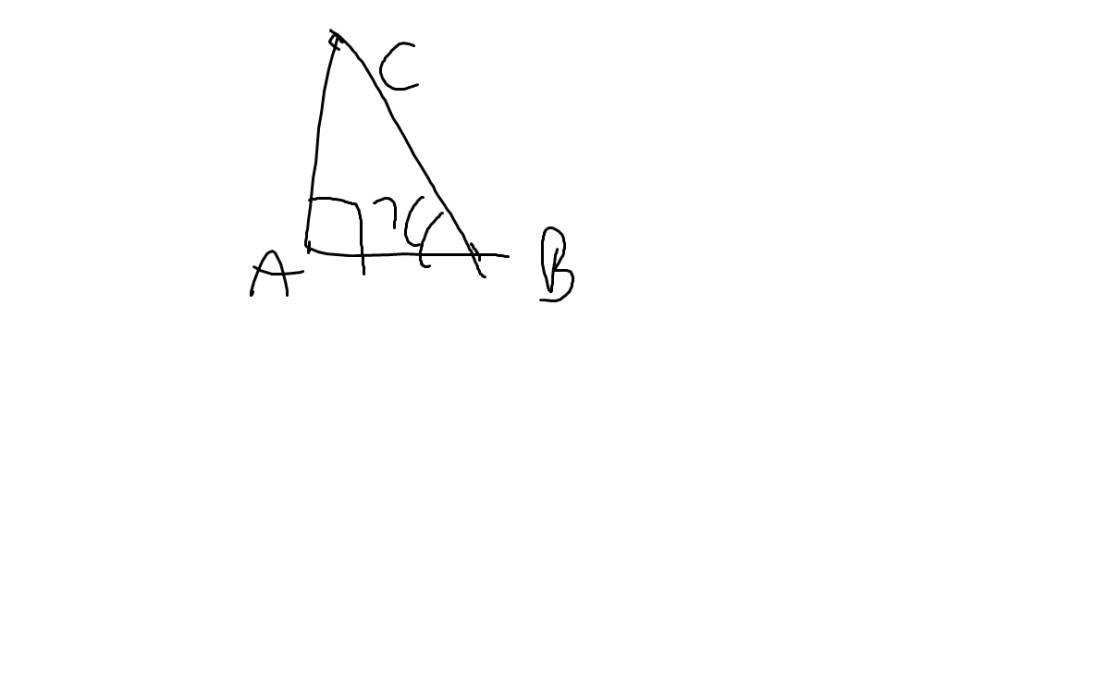
Đặt \(x=\widehat{B}\)
sin x=sin B=AC/BC
cosx=cosB=AB/BC
\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)
=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)
b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)
30 tháng 7 2023
\(=\dfrac{tan\left(\dfrac{pi}{2}+x\right)\cdot sin\left(-x\right)\cdot cos\left(x-pi\right)}{cos\left(\dfrac{pi}{2}-x\right)\cdot sin\left(x+pi\right)}\)
\(=\dfrac{-cotx\cdot sin\left(-x\right)\cdot\left(-cosx\right)}{sinx\cdot-sinx}\)
\(=\dfrac{cotx\cdot sinx\left(-1\right)\cdot cosx}{-sinx\cdot sinx}=\dfrac{\dfrac{cosx}{sinx}\cdot cosx}{sinx}=\dfrac{cos^2x}{sin^2x}=cot^2x\)
Cho biết \(cosx=-\dfrac{1}{2}\)
\(sin^2x+cos^2x=1\Rightarrow sin^2x=1-cos^2x\)
\(\Rightarrow sin^2x=1-\dfrac{1}{4}=\dfrac{3}{4}\)
\(S=4sin^2x+8tan^2x\)
\(\Rightarrow S=4\left(sin^2x+2\dfrac{sin^2x}{cos^2x}\right)\)
\(\Rightarrow S=4\left(\dfrac{3}{4}+2\dfrac{\dfrac{3}{4}}{\dfrac{1}{4}}\right)\)
\(\Rightarrow S=4\left(\dfrac{3}{4}+6\right)\)
\(\Rightarrow S=4.\dfrac{27}{4}=27\)