Hãy tìm một biến cố khác rỗng và xung khắc với cả ba biến cố \(A,B\) và \(C\) trong Ví dụ 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(D = \left\{ {\left( {3;1} \right);\left( {3;2} \right);\left( {3;3} \right);\left( {3;4} \right);\left( {3;5} \right);\left( {3;6} \right)} \right\}\)
\(A{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};B{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};C{\rm{D}} = \left\{ {\left( {3;1} \right)} \right\}\)
b) \(\bar AB = \left\{ {\left( {1;6} \right);\left( {6;1} \right)} \right\}\)
\(\bar A{\rm{C}} = \left\{ {\left( {1;6} \right);\left( {6;1} \right);\left( {1;5} \right);\left( {5;1} \right);\left( {1;3} \right);\left( {3;1} \right);\left( {1;2} \right);\left( {2;1} \right);\left( {1;1} \right)} \right\}\)

Ak là biến cố: "Người thứ k bắn trúng"
- A1 : "Người thứ nhất bắn trúng"
⇒ 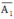 : “Người thứ nhất không bắn trúng”.
: “Người thứ nhất không bắn trúng”.
- A2 : "Người thứ hai bắn trúng"
⇒ 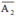 : “Người thứ hai không bắn trúng”.
: “Người thứ hai không bắn trúng”.


Số kết quả thuận lợi cho biến cố \(A \cup B\) là \(5 + 12 = 17\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{{n\left( \Omega \right)}};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega\right)}} = \frac{{12}}{{n\left( \Omega\right)}};P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega\right)}} = \frac{{17}}{{n\left( \Omega\right)}}\)
\( \Rightarrow P\left( A \right) + P\left( B \right) = P\left( {A \cup B} \right)\)

Hai biến cố A và B xung khắc khi và chỉ khi \(A \cap B = \emptyset \Rightarrow P\left( {AB} \right) = 0\)
Vì P(A) > 0, P(B) > 0 nên \(P\left( A \right).P\left( B \right) > 0\)
\( \Rightarrow P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\)
Vậy hai biến cố A và B không độc lập.

a) Hai biến cố đối nhau không có xung khắc với nhau. Xung khắc xảy ra khi hai biến cố không thể xảy ra cùng một lúc.
b) Hai biến cố xung khắc không nhất thiết là hai biến cố đối nhau. Hai biến cố đối nhau xảy ra khi xảy ra một biến cố sẽ loại trừ hoàn toàn biến cố kia.
$HaNa$

Hai biến cố này có xung khắc vì \(\Omega=A\cup\overline{A}\)

Biến cố A: "Cả 3 lần xuất hiện mặt sấp"
=>\(A=\left\{A_1;A_2;A_3\right\}\)
Biến cố B: "Cả 3 lần xuất hiện mặt ngửa"
=>\(B=\left\{\overline{A_1};\overline{A_2};\overline{A_3}\right\}\)

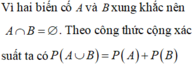
THAM KHẢO:
Biến cố D "Tích số chấm xuất hiện trên hai con xúc xắc là 10"