Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).
a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).
b) Tính thể tích của khối hộp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 8 2018
Đáp án là C.
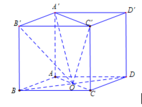
Ta có: V O . A , B , C , = 1 2 V O . A , B , C , D , ; V O . A , B , C , D , 1 3 V A B C D . A , B , C , D ,
V O . A , B , C , = 1 6 V A B C D . A , B , C , D , ⇒ V O . A , B , C , V A B C D . A , B , C , D = 1 6
a) Gọi \(O = AC \cap B{\rm{D}}\)
\(ABCD\) là hình thoi \( \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}\)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AO\)
\( \Rightarrow d\left( {B{\rm{D}},AA'} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
b) Tam giác \(OAB\) vuông tại \(O\)
\(\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A'B'C'}} = {S_{ABC{\rm{D}}}}.AA' = \frac{{3{a^3}}}{4}\end{array}\)